
【题目】已知椭圆C: ![]() =1,(a>b>0)的离心率为
=1,(a>b>0)的离心率为 ![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+
,以原点为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+ ![]() =0)且不垂直于x轴直线l椭圆C相交于A、B两点. (Ⅰ)求椭圆C的方程;
=0)且不垂直于x轴直线l椭圆C相交于A、B两点. (Ⅰ)求椭圆C的方程;
(Ⅱ)求 ![]()
![]() 取值范围;
取值范围;
(Ⅲ)若B关于x轴的对称点是E,证明:直线AE与x轴相交于定点.
【答案】解:(Ⅰ)由题意知 ![]() ,∴
,∴ ![]() ,即
,即 ![]() , 又
, 又 ![]() ,∴a2=4,b2=3,
,∴a2=4,b2=3,
故椭圆的方程为 ![]() ;
;
(Ⅱ)解:由题意知直线l的斜率存在,设直线l的方程为y=k(x﹣4),
由  得:(4k2+3)x2﹣32k2x+64k2﹣12=0.
得:(4k2+3)x2﹣32k2x+64k2﹣12=0.
由△=(﹣32k2)2﹣4(4k2+3)(64k2﹣12)>0得: ![]() .
.
设A(x1 , y1),B (x2 , y2),则 ![]() ,
, ![]() ①
①
∴y1y2=k(x1﹣4)k(x2﹣4)= ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,则
,则 ![]() .
.
∴ ![]() 的取值范围是
的取值范围是 ![]() ;
;
(Ⅲ)证明:∵B、E两点关于x轴对称,∴E(x2 , ﹣y2),
直线AE的方程 ![]() ,令y=0,得
,令y=0,得 ![]() ,
,
又y1=k(x1﹣4),y2=k(x2﹣4),
∴ ![]() ,
,
将①代入上式并整理得:x=1,
∴直线AE与x轴交于定点(1,0)
【解析】(Ⅰ)由椭圆的离心率得到a,b的关系式 ![]() ,由原点到直线x﹣y+
,由原点到直线x﹣y+ ![]() =0的距离求得b,则a可求,椭圆方程可求;(Ⅱ)由题意知直线l的斜率存在,设直线l的方程为y=k(x﹣4),联立直线方程与椭圆方程,由△>0得k的范围,利用根与系数的关系得到A,B两点的横坐标的和与积,代入
=0的距离求得b,则a可求,椭圆方程可求;(Ⅱ)由题意知直线l的斜率存在,设直线l的方程为y=k(x﹣4),联立直线方程与椭圆方程,由△>0得k的范围,利用根与系数的关系得到A,B两点的横坐标的和与积,代入 ![]()
![]() ,结合k的范围可得
,结合k的范围可得 ![]()
![]() 取值范围;(Ⅲ)由B、E两点关于x轴对称,得到E(x2 , ﹣y2),写出直线AE的方程,求出直线在x轴上的截距x=1,则可说明直线AE与x轴交于定点(1,0).
取值范围;(Ⅲ)由B、E两点关于x轴对称,得到E(x2 , ﹣y2),写出直线AE的方程,求出直线在x轴上的截距x=1,则可说明直线AE与x轴交于定点(1,0).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】古希腊亚历山大时期的数学家帕普斯(Pappus,约300~约350)在《数学汇编》第3卷中记载着一个定理:“如果同一平面内的一个闭合图形的内部与一条直线不相交,那么该闭合图形围绕这条直线旋转一周所得到的旋转体的体积等于闭合图形面积乘以重心旋转所得周长的积.”如图,半圆![]() 的直径
的直径![]() ,点
,点![]() 是该半圆弧的中点,半圆弧与直径
是该半圆弧的中点,半圆弧与直径![]() 所围成的半圆面(阴影部分不含边界)的重心
所围成的半圆面(阴影部分不含边界)的重心![]() 位于对称轴
位于对称轴![]() 上.若半圆面绕直径
上.若半圆面绕直径![]() 所在直线旋转一周,则所得到的旋转体的体积为__________
所在直线旋转一周,则所得到的旋转体的体积为__________![]() ,
,![]() ___________________
___________________![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知球O是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)A-BCD的外接球,BC=3,![]() ,点E在线段BD上,且BD=3BE,过点E作圆O的截面,则所得截面圆面积的取值范围是__.
,点E在线段BD上,且BD=3BE,过点E作圆O的截面,则所得截面圆面积的取值范围是__.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015男篮亚锦赛决赛阶段,中国男篮以9连胜的不败战绩赢得第28届亚锦赛冠军,同时拿到亚洲唯一1张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛MVP(最有价值球员),下表是易建联在这9场比赛中投篮的统计数据.
比分 | 易建联技术统计 | |||
投篮命中 | 罚球命中 | 全场得分 | 真实得分率 | |
中国91﹣42新加坡 | 3/7 | 6/7 | 12 | 59.52% |
中国76﹣73韩国 | 7/13 | 6/8 | 20 | 60.53% |
中国84﹣67约旦 | 12/20 | 2/5 | 26 | 58.56% |
中国75﹣62哈萨克期坦 | 5/7 | 5/5 | 15 | 81.52% |
中国90﹣72黎巴嫩 | 7/11 | 5/5 | 19 | 71.97% |
中国85﹣69卡塔尔 | 4/10 | 4/4 | 13 | 55.27% |
中国104﹣58印度 | 8/12 | 5/5 | 21 | 73.94% |
中国70﹣57伊朗 | 5/10 | 2/4 | 13 | 55.27% |
中国78﹣67菲律宾 | 4/14 | 3/6 | 11 | 33.05% |
注:(1)表中a/b表示出手b次命中a次;
(2)TS%(真实得分率)是衡量球员进攻的效率,其计算公式为:
TS%=.全场得分/2x(投篮出手次数+0.44x罚球出手次数)
(Ⅰ)从上述9场比赛中随机选择一场,求易建联在该场比赛中TS%超过50%的概率;
(Ⅱ)从上述9场比赛中随机选择两场,求易建联在这两场比赛中TS%至少有一场超过60%的概率;
(Ⅲ)用x来表示易建联某场的得分,用y来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断y与x之间是否具有线性相关关系?结合实际简单说明理由.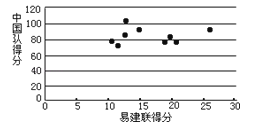
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com