
分析 设A(x,y),则B(-x,-y)根据向量坐标关系,利用换元法转化为一元二次函数,利用一元二次函数的性质进行求解即可.
解答 解:设A(x,y),则B(-x,-y),
则$\overrightarrow{PA}$•$\overrightarrow{PB}$=(x,y-3)•(-x,-y-3)=-x2-(y-3)(y+3)=-x2-y2+9,
∵A是椭圆$\frac{{x}^{2}}{4}$+y2=1上的任意一点,
∴$\frac{{x}^{2}}{4}$+y2=1,即y2=1-$\frac{{x}^{2}}{4}$,-2≤x≤2,
则$\overrightarrow{PA}$•$\overrightarrow{PB}$=-x2-y2+9=-x2-(1-$\frac{{x}^{2}}{4}$)+9=-$\frac{3{x}^{2}}{4}$+8,
∵-2≤x≤2,
∴当x=0时,$\overrightarrow{PA}$•$\overrightarrow{PB}$最大,此时$\overrightarrow{PA}$•$\overrightarrow{PB}$=8,
当x=2或-2时,$\overrightarrow{PA}$•$\overrightarrow{PB}$最小,此时$\overrightarrow{PA}$•$\overrightarrow{PB}$=8-3=5,
即5≤$\overrightarrow{PA}$•$\overrightarrow{PB}$≤8,
故答案为:[5,8]
点评 本题主要考查椭圆性质的应用,利用向量数量积的坐标公式,利用消元法转化为一元二次函数是解决本题的关键.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:解答题
| x | 6 | 8 | 10 | 12 |
| y | 3 | 4 | 6 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
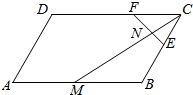 如图平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{d}$,F是CD的三等分点,E是BC中点,M是AB中点,MC∩EF=N,若$\overrightarrow{MN}$=λ1$\overrightarrow{b}$+λ2$\overrightarrow{d}$,则λ1+λ2=( )
如图平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{d}$,F是CD的三等分点,E是BC中点,M是AB中点,MC∩EF=N,若$\overrightarrow{MN}$=λ1$\overrightarrow{b}$+λ2$\overrightarrow{d}$,则λ1+λ2=( )| A. | $\frac{15}{14}$ | B. | 1 | C. | $\frac{5}{14}$ | D. | -$\frac{5}{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
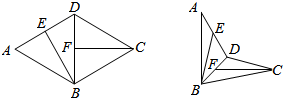 如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( )
如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( )| A. | ($\frac{π}{6}$,$\frac{π}{3}$) | B. | ($\frac{π}{6}$,$\frac{π}{2}$] | C. | ($\frac{π}{3}$,$\frac{π}{2}$] | D. | ($\frac{π}{3}$,$\frac{2π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -$\frac{1}{4}$ | C. | -4或-$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{2}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-y-1=0 | B. | 3x-y-5=0 | C. | 3x-y+5=0 | D. | 3x+y-1=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com