
【题目】已知棱长为l的正方体![]() 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、![]() 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段![]() 上,且
上,且![]() ,设面
,设面![]() 面MPQ=
面MPQ=![]() ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )

A.![]() 面ABCD
面ABCD
B.![]() AC
AC
C.面MEF与面MPQ不垂直
D.当x变化时,![]() 不是定直线
不是定直线
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点,焦点在![]() 轴上的椭圆,离心率为
轴上的椭圆,离心率为![]() 且过点
且过点![]() ,过定点
,过定点![]() 的动直线与该椭圆相交于
的动直线与该椭圆相交于![]() 、
、![]() 两点.
两点.
(1)若线段![]() 中点的横坐标是
中点的横坐标是![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为常数?若存在,求出点
为常数?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们知道,如果集合AS,那么S的子集A的补集为SA={x|x∈S,且xA}.类似地,对于集合A、B,我们把集合{x|x∈A,且xB}叫作集合A与B的差集,记作A-B.据此回答下列问题:
(1)若A={1,2,3,4},B={3,4,5,6},求A-B;
(2)在下列各图中用阴影表示集合A-B.
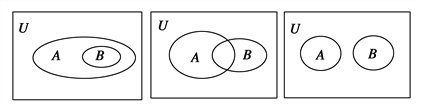
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x-1|+|x-2a|.
(1)当a=1时,求f(x)≤3的解集;
(2)当x∈[1,2]时,f(x)≤3恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
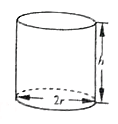
【题目】某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计).易拉罐的体积为![]()
![]() ,设圆柱的高度为
,设圆柱的高度为![]()
![]() ,底面半径为
,底面半径为![]()
![]() ,且
,且![]() .假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为
.假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为![]() 元/
元/ ![]() ,易拉罐上下底面的制造费用均为
,易拉罐上下底面的制造费用均为![]() 元/
元/ ![]() (
(![]() ,
, ![]() 为常数,且
为常数,且![]() ).
).
(1)写出易拉罐的制造费用![]() (元)关于
(元)关于![]() 的函数表达式,并求其定义域;
的函数表达式,并求其定义域;
(2)求易拉罐制造费用最低时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数![]() (m∈Z)为偶函数,且在区间(0,+∞)上是单调增函数.
(m∈Z)为偶函数,且在区间(0,+∞)上是单调增函数.
(1)求函数f(x)的解析式;
(2)设函数![]() ,若g(x)>2对任意的x∈R恒成立,求实数c的取值范围.
,若g(x)>2对任意的x∈R恒成立,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+a2.
(I)若f(x)在x=1处有极值10,求a,b的值;
(II)若当a=-1时,f(x)<0在x∈[1,2]恒成立,求b的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a是实数,函数f(x)=![]() (x-a).
(x-a).
(1)求函数f(x)的单调区间;
(2)设g(a)为f(x)在区间[0,2]上的最小值.
①写出g(a)的表达式;
②求a的取值范围,使得-6≤g(a)≤-2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有2个红球,4个白球,除颜色外,它们的形状、大小、质量等完全相同
(1)采用不放回抽样,先后取两次,每次随机取一个球,求恰好取到1个红球,七个白球的概率;
(2)采用放回抽样,每次随机抽取一球,连续取3次,求至少有1次取到红球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com