
【题目】已知![]() ,
,![]() ,其中
,其中![]() 为实常数.
为实常数.
(1)若函数![]() 在区间[2,3]上为单调递增函数,求
在区间[2,3]上为单调递增函数,求![]() 的取值范围;
的取值范围;
(2)高函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,试讨论函数
,试讨论函数![]() ,
,![]() 的零点的情况.
的零点的情况.
科目:高中数学 来源: 题型:
【题目】疫情期间口罩需求量大增,某医疗器械公司开始生产KN95口罩,并且对所生产口罩的质量按指标测试分数进行划分,其中分数不小于70的为合格品,否则为不合格品,现随机抽取100件口罩进行检测,其结果如下:

(1)根据表中数据,估计该公司生产口罩的不合格率;
(2)根据表中数据,估计该公司口罩的平均测试分数;
(3)若用分层抽样的方式按是否合格从所生产口罩中抽取5件,再从这5件口罩中随机抽取2件,求这2件口罩全是合格品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用合适的方法表示下列集合,并说明是有限集还是无限集.
(1)到A、B两点距离相等的点的集合
(2)满足不等式![]() 的
的![]() 的集合
的集合
(3)全体偶数
(4)被5除余1的数
(5)20以内的质数
(6)![]()
(7)方程![]() 的解集
的解集
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某辆汽车以![]() 千米/小时的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求
千米/小时的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求![]() )时,每小时的油耗(所需要的汽油量)为
)时,每小时的油耗(所需要的汽油量)为![]() 升,其中
升,其中![]() 为常数,且
为常数,且![]() .
.
(1)若汽车以![]() 千米/小时的速度行驶时,每小时的油耗为
千米/小时的速度行驶时,每小时的油耗为![]() 升,欲使每小时的油耗不超过
升,欲使每小时的油耗不超过![]() 升,求
升,求![]() 的取值范围;
的取值范围;
(2)求该汽车行驶![]() 千米的油耗的最小值.
千米的油耗的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
⑴若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
⑵当![]() ,求函数
,求函数![]() 的最小值
的最小值![]() ;
;
⑶是否存在实数![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》 是我国古代的天文学和数学著作。其中一个问题的大意为:一年有二十四个节气(如图),每个节气晷长损益相同(即物体在太阳的照射下影子长度的增加量和减少量相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:ー丈等于十尺,一尺等于十寸),则立冬节气的晷长为( )
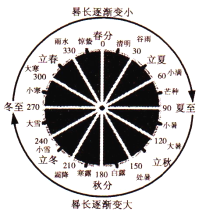
A. 九尺五寸 B. 一丈五寸 C. 一丈一尺五寸 D. 一丈六尺五寸
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com