
 ,
, 为一平面内两非零向量,则
为一平面内两非零向量,则 ⊥
⊥ 是|
是|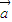 +
+ |=|
|=|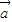 -
- |的充要条件;
|的充要条件; =2,则b=-1.
=2,则b=-1. +
+ |=|
|=| -
- |平方,化简可得
|平方,化简可得 ⊥
⊥ ;②把点P(x,y)的坐标代入方程f1(x,y)+f2(x,y)=0可得证;③用反证法可证;④把b=-1代入
;②把点P(x,y)的坐标代入方程f1(x,y)+f2(x,y)=0可得证;③用反证法可证;④把b=-1代入 验证,可证.
验证,可证. +
+ |=
|= ,|
,| -
- |=
|=
 +
+ |=|
|=| -
- |∴
|∴

 ⊥
⊥ ;必要性:∵
;必要性:∵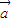 ⊥
⊥ ;∴
;∴

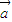 +
+ |=|
|=| -
- |
|
 =2,∴b=-1
=2,∴b=-1

科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:云南省红河哈尼族彝族自治州蒙自县高级中学2006-2007学年度高三数学理科第一次月考试卷 题型:013
⊥∥已知两直线m、n,两平面α、β,且m⊥α,n![]() β.下面有四个命题:(1)若α∥β,则有m⊥n;(2)若m⊥n,则有α∥β;(3)若m∥n,则有α⊥β;(4)若α⊥β,则有m∥n.其中正确命题的个数是:
β.下面有四个命题:(1)若α∥β,则有m⊥n;(2)若m⊥n,则有α∥β;(3)若m∥n,则有α⊥β;(4)若α⊥β,则有m∥n.其中正确命题的个数是:
A.3
B.1
C.4
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com