
ΓΨΧβΡΩΓΩΡ≥¥σ―ß‘ΎΩΣ―ßΦΨΉΦ±Ηœζ έ“Μ÷÷Κ–ΖΙΫχ–– ‘¥¥“ΒΘ§‘Ύ“ΜΗωΩΣ―ßΦΨΡΎΘ§ΟΩ έ≥ω1Κ–ΗΟΚ–ΖΙΜώάϊ»σ10‘ΣΘ§Έ¥ έ≥ωΒΡ≤ζΤΖΘ§ΟΩΚ–ΩςΥπ5‘ΣΘ°ΗυΨίάζ ΖΉ ΝœΘ§ΒΟΒΫΩΣ―ßΦΨ –≥Γ–η«σΝΩΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§»γΆΦΥυ ΨΘ°ΗΟΆ§―ßΈΣ’βΗωΩΣ―ßΦΨΙΚΫχΝΥ150Κ–ΗΟ≤ζΤΖΘ§“‘![]() Θ®ΒΞΈΜΘΚΚ–Θ§
Θ®ΒΞΈΜΘΚΚ–Θ§![]() Θ©±μ Ψ’βΗωΩΣ―ßΦΨΡΎΒΡ –≥Γ–η«σΝΩΘ§
Θ©±μ Ψ’βΗωΩΣ―ßΦΨΡΎΒΡ –≥Γ–η«σΝΩΘ§![]() Θ®ΒΞΈΜΘΚ‘ΣΘ©±μ Ψ’βΗωΩΣ―ßΦΨΡΎΨ≠œζΗΟ≤ζΤΖΒΡάϊ»σΘ°
Θ®ΒΞΈΜΘΚ‘ΣΘ©±μ Ψ’βΗωΩΣ―ßΦΨΡΎΨ≠œζΗΟ≤ζΤΖΒΡάϊ»σΘ°
Θ®ΔώΘ©ΗυΨί÷±ΖΫΆΦΙάΦΤ’βΗωΩΣ―ßΦΨΡΎ –≥Γ–η«σΝΩ![]() ΒΡΤΫΨυ ΐΚΆ÷Ύ ΐΘΜ
ΒΡΤΫΨυ ΐΚΆ÷Ύ ΐΘΜ
Θ®ΔρΘ©ΫΪ![]() ±μ ΨΈΣ
±μ ΨΈΣ![]() ΒΡΚ· ΐΘΜ
ΒΡΚ· ΐΘΜ
Θ®ΔσΘ©ΗυΨίΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΙάΦΤάϊ»σ![]() ≤Μ…Ό”Ύ1350‘ΣΒΡΗ≈¬ Θ°
≤Μ…Ό”Ύ1350‘ΣΒΡΗ≈¬ Θ°
ΓΨ¥πΑΗΓΩΘ®ΔώΘ©ΤΫΨυ ΐΈΣ153Θ§÷Ύ ΐΈΣ150; Θ®ΔρΘ©![]() Θ§
Θ§![]() ; Θ®ΔσΘ©0.7.
; Θ®ΔσΘ©0.7.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚ
(1)ΫαΚœΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΩ…ΒΟΤΫΨυ ΐ![]() Θ§‘ΡΕΝ÷±ΖΫΆΦΩ…ΒΟ÷Ύ ΐΈΣ150.
Θ§‘ΡΕΝ÷±ΖΫΆΦΩ…ΒΟ÷Ύ ΐΈΣ150.
(2)”…Χβ“βΩ…ΫΪΚ· ΐ–¥≥…Ζ÷ΕΈΚ· ΐΒΡ–Έ ΫΘΚ ![]() Θ§
Θ§ ![]() ;
;
(3)άϊ”ΟΧβ“βΝ–≥ω≤ΜΒ» ΫΘ§ΫαΚœ(1)ΒΡΫα¬έΩ…ΒΟάϊ»σ![]() ≤Μ…Ό”Ύ1350‘ΣΒΡΗ≈¬ ΈΣ0.7.
≤Μ…Ό”Ύ1350‘ΣΒΡΗ≈¬ ΈΣ0.7.
‘ΧβΫβΈωΘΚ
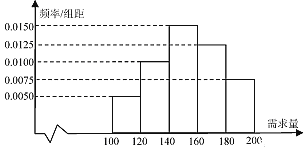
Θ®ΔώΘ©”…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΒΟΘΚΉν¥σ–η«σΝΩΈΣ150Κ–ΒΡΤΒ¬ ΈΣ![]() .
.
’βΗωΩΣ―ßΦΨΡΎ –≥Γ–η«σΝΩΒΡ÷Ύ ΐΙάΦΤ÷Β «150.
–η«σΝΩΈΣ[100,120Θ©ΒΡΤΒ¬ ΈΣ![]() Θ§
Θ§
–η«σΝΩΈΣ[120,140Θ©ΒΡΤΒ¬ ΈΣ![]() Θ§
Θ§
–η«σΝΩΈΣ[140,160Θ©ΒΡΤΒ¬ ΈΣ![]() Θ§
Θ§
–η«σΝΩΈΣ[160,180Θ©ΒΡΤΒ¬ ΈΣ![]() Θ§
Θ§
–η«σΝΩΈΣ[180,200Θ©ΒΡΤΒ¬ ΈΣ![]() Θ§
Θ§
‘ρΤΫΨυ ΐ
![]()
![]() .
.
‘ΡΕΝ÷±ΖΫΆΦΩ…ΒΟ÷Ύ ΐΈΣ150.
Θ®ΔρΘ©“ρΈΣΟΩ έ≥ω1Κ–ΗΟΚ–ΖΙΜώάϊ»σ10‘ΣΘ§Έ¥ έ≥ωΒΡΚ–ΖΙΘ§ΟΩΚ–ΩςΥπ5‘ΣΘ§
Υυ“‘Β±![]() ±Θ§
±Θ§![]()
![]() Θ§
Θ§
Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§
Υυ“‘![]() Θ§
Θ§![]() .
.
Θ®ΔσΘ©“ρΈΣάϊ»σ≤Μ…Ό”Ύ1350‘ΣΘ§Υυ“‘![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() .
.
Υυ“‘”…Θ®ΔώΘ©÷Σάϊ»σ≤Μ…Ό”Ύ1350‘ΣΒΡΗ≈¬ ![]() .
.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΝΫΗωΖ«ΝψœρΝΩ ![]() ΓΔ
ΓΔ ![]() ≤ΜΙ≤œΏΘ°
≤ΜΙ≤œΏΘ°
Θ®1Θ©»τ ![]() =
= ![]() +
+ ![]() Θ§
Θ§ ![]() =2
=2 ![]() +8
+8 ![]() Θ§
Θ§ ![]() =3Θ®
=3Θ® ![]() ©¹
©¹ ![]() Θ©Θ§«σ÷ΛΘΚAΓΔBΓΔD»ΐΒψΙ≤œΏΘΜ
Θ©Θ§«σ÷ΛΘΚAΓΔBΓΔD»ΐΒψΙ≤œΏΘΜ
Θ®2Θ©«σ Β ΐk Ιk ![]() +
+ ![]() ”κ2
”κ2 ![]() +k
+k ![]() Ι≤œΏΘ°
Ι≤œΏΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©Ε‘»Έ“β Β ΐxΘ§y¬ζΉψfΘ®xΘ©+fΘ®yΘ©=fΘ®x+yΘ©+3Θ§fΘ®3Θ©=6Θ§Β±xΘΨ0 ±Θ§fΘ®xΘ©ΘΨ3Θ§Ρ«Ο¥Θ§Β±fΘ®2a+1Θ©ΘΦ5 ±Θ§ Β ΐaΒΡ»Γ÷ΒΖΕΈß «
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΗυΨίΧβ“βΫβ¥π
Θ®1Θ©«σΕ®ΜΐΖ÷ ![]() |x2©¹2|dxΒΡ÷ΒΘΜ
|x2©¹2|dxΒΡ÷ΒΘΜ
Θ®2Θ©»τΗ¥ ΐz1=a+2iΘ®aΓ RΘ©Θ§z2=3©¹4iΘ§«“ ![]() ΈΣ¥Ω–ι ΐΘ§«σ|z1|
ΈΣ¥Ω–ι ΐΘ§«σ|z1|
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΚ÷ΣfΘ®xΘ©=x2©¹2x+2Θ§‘Ύ[ ![]() Θ§m2©¹m+2]…œ»Έ»Γ»ΐΗω ΐaΘ§bΘ§cΘ§Ψυ¥φ‘Ύ“‘ fΘ®aΘ©Θ§fΘ®bΘ©Θ§fΘ®cΘ©ΈΣ»ΐ±ΏΒΡ»ΐΫ«–ΈΘ§‘ρmΒΡ»Γ÷ΒΖΕΈßΈΣΘ® Θ©
Θ§m2©¹m+2]…œ»Έ»Γ»ΐΗω ΐaΘ§bΘ§cΘ§Ψυ¥φ‘Ύ“‘ fΘ®aΘ©Θ§fΘ®bΘ©Θ§fΘ®cΘ©ΈΣ»ΐ±ΏΒΡ»ΐΫ«–ΈΘ§‘ρmΒΡ»Γ÷ΒΖΕΈßΈΣΘ® Θ©
A.Θ®0Θ§1Θ©
B.[0Θ§ ![]() Θ©
Θ©
C.Θ®0Θ§ ![]() ]
]
D.[ ![]() Θ§
Θ§ ![]() ]
]
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() Θ§«ζœΏ
Θ§«ζœΏ![]() …œ»Έ“β“ΜΒψ
…œ»Έ“β“ΜΒψ![]() ¬ζΉψ
¬ζΉψ![]() ΘΜ«ζœΏ
ΘΜ«ζœΏ![]() …œΒΡΒψ
…œΒΡΒψ![]() ‘Ύ
‘Ύ![]() ÷αΒΡ”“±Ώ«“
÷αΒΡ”“±Ώ«“![]() ΒΫ
ΒΫ![]() ΒΡΨύάκ”κΥϋΒΫ
ΒΡΨύάκ”κΥϋΒΫ![]() ÷αΒΡΨύάκΒΡ≤νΈΣ1Θ°
÷αΒΡΨύάκΒΡ≤νΈΣ1Θ°
Θ®1Θ©«σ![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©Ιΐ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() ”κ
”κ![]() œύΫΜ”ΎΒψ
œύΫΜ”ΎΒψ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() Ζ÷±π”κ
Ζ÷±π”κ![]() œύΫΜ”ΎΒψ
œύΫΜ”ΎΒψ![]() ΚΆ
ΚΆ![]() Θ°«σ
Θ°«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ![]() «ΑκΨΕΈΣ2ΒΡΑκ«ρ
«ΑκΨΕΈΣ2ΒΡΑκ«ρ![]() ΒΡ÷±ΨΕΘ§
ΒΡ÷±ΨΕΘ§ ![]() ΈΣ«ρΟφ…œΒΡΝΫΒψ«“
ΈΣ«ρΟφ…œΒΡΝΫΒψ«“![]() Θ§
Θ§ ![]() Θ°
Θ°
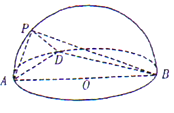
Θ®1Θ©«σ÷ΛΘΚΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©«σΕΰΟφΫ«![]() ΒΡ”ύœ“÷ΒΘ°
ΒΡ”ύœ“÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤![]() ΒΡάκ–Ρ¬ ΈΣ
ΒΡάκ–Ρ¬ ΈΣ![]() Θ§«“ΙΐΒψ
Θ§«“ΙΐΒψ Θ°
Θ°
Θ®1Θ©«σ![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ© «Ζώ¥φ‘Ύ÷±œΏ![]() ”κ
”κ![]() œύΫΜ”Ύ
œύΫΜ”Ύ![]() ΝΫΒψΘ§«“¬ζΉψΘΚΔΌ
ΝΫΒψΘ§«“¬ζΉψΘΚΔΌ![]() ”κ
”κ![]() Θ®
Θ®![]() ΈΣΉχ±ξ‘≠ΒψΘ©ΒΡ–±¬ ÷°ΚΆΈΣ2ΘΜΔΎ÷±œΏ
ΈΣΉχ±ξ‘≠ΒψΘ©ΒΡ–±¬ ÷°ΚΆΈΣ2ΘΜΔΎ÷±œΏ![]() ”κ‘≤
”κ‘≤![]() œύ«–Θ§»τ¥φ‘ΎΘ§«σ≥ω
œύ«–Θ§»τ¥φ‘ΎΘ§«σ≥ω![]() ΒΡΖΫ≥ΧΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΒΡΖΫ≥ΧΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΑ―Κ· ΐfΘ®xΘ©=sinΘ®2x+Π’Θ©ΒΡΆΦœσœρΉσΤΫ“Τ ![]() ΗωΒΞΈΜΚσΘ§ΥυΒΟΆΦœσΙΊ”Ύy÷αΕ‘≥ΤΘ§‘ρΠ’Ω…“‘ΈΣΘ® Θ©
ΗωΒΞΈΜΚσΘ§ΥυΒΟΆΦœσΙΊ”Ύy÷αΕ‘≥ΤΘ§‘ρΠ’Ω…“‘ΈΣΘ® Θ©
A.![]()
B.![]()
C.![]()
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com