练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知B岛在A岛正东方向距离12km处，C岛在A岛北偏东方向相离8km处．某船从A岛出发向B岛驶去，并在与B，C距离相等处待命．

    （1）求此船航行的距离（精确到0.1km）．

    （2）若此船在待命处接到命令，以最少的时间行驶到C岛，则此船应沿什么方向行驶？

    【答案】(1) 7.9km (2) 北偏西方向

    【解析】

    根据题意作出示意图，设此船向岛方向行驶到处时，．设，则有．

    （1）在中，利用余弦定理，即可解得此船航行的距离，

    （2）结合（1）的结论，在中，利用余弦定理，求得，从而得到船行驶的方向．

    作出示意图，如图所示．

    设此船向岛方向行驶到处时，．设，

    则有．

    （1）在中，，，，．

    由余弦定理，得，解得，

    ，即此船从岛到待命处应该航行的距离约为．

    （2）由余弦定理，得．

    ，即船应沿北偏西方向全速行驶就可尽快到达岛．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到频数分布表和频率分布直方图如下．

    组号

    分组

    频数

    1

    [0，2）

    6

    2

    [2，4）

    8

    3

    [4，6）

    17

    4

    [6，8）

    22

    5

    [8，10）

    25

    6

    [10，12）

    12

    7

    [12，14）

    6

    8

    [14，16）

    2

    9

    [16，18）

    2

    合计

    100

    （1）从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的频率；

    （2）求频率分布直方图中的a，b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从一张半径为3的圆形铁皮中裁剪出一块扇形铁皮（如图1阴影部分），并卷成一个深度为米的圆锥筒（如图2）.若所裁剪的扇形铁皮的圆心角为.

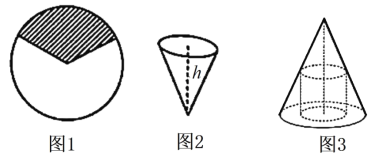
    （1）求圆锥筒的容积；

    （2）在（1）中的圆锥内有一个底面圆半径为的内接圆柱（如图3），求内接圆柱侧面积最大时的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点A(0，－2)，椭圆E： (a>b>0)的离心率为，F是椭圆E的右焦点，直线AF的斜率为，O为坐标原点.

    (1)求E的方程；

    (2)设过点A的动直线l与E相交于P，Q两点.当△OPQ的面积最大时，求l的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等比数列中，依次是某等差数列的第5项、第3项、第2项，且，公比

    （1）求；

    （2）设，求数列的前项和

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市户居民的月平均用电量（单位：度），以，，，，，，分组的频率分布直方图如图．

    （1）求直方图中的值；

    （2）求月平均用电量的众数和中位数；

    （3）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取户居民，则月平均用电量在的用户中应抽取多少户？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知不等式.

    （1）是否存在实数m，使不等式对任意恒成立？并说明理由.

    （2）若不等式对任意恒成立，求实数m的取值范围.

    （3）若对于，不等式恒成立，求实数x的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，且椭圆上一点P的坐标为.

    （1）求椭圆M的方程；

    （2）设椭圆的右顶点为C，不经过点C的直线l与椭圆M交于A，B两点，且以线段AB为直径的圆过点C，

    ①证明：直线l过定点，并求出该定点坐标；

    ②求面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数的定义域为D，若存在闭区间，使得函数满足以下两个条件：（1）在[m，n]上是单调函数；（2）在[m，n]上的值域为[2m，2n]，则称区间[m，n]为的“倍值区间”.下列函数中存在“倍值区间”的有（ ）个.

    ①②③

    A.0B.1C.2D.3

    查看答案和解析>>

    同步练习册答案