
分析 sin2x>cos2x,化为cos2x<0,利用余弦函数的图象与性质即可得出.
解答 解:∵sin2x>cos2x,
∴cos2x<0,
∴2kπ+$\frac{π}{2}$<2x$<\frac{3π}{2}$+2kπ,
解得kπ+$\frac{π}{4}$<x<$\frac{3π}{4}$+kπ(k∈Z).
∴x的取值范围是(kπ+$\frac{π}{4}$,$\frac{3π}{4}$+kπ)(k∈Z).
故答案为:(kπ+$\frac{π}{4}$,$\frac{3π}{4}$+kπ)(k∈Z).
点评 本题考查了余弦函数的图象与性质、倍角公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
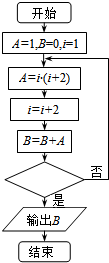 如图给出的是计算1×3+3×5+5×7+…+13×15的值的一个程序框图,其中判断框内应填入的条件不正确的是( )
如图给出的是计算1×3+3×5+5×7+…+13×15的值的一个程序框图,其中判断框内应填入的条件不正确的是( )| A. | i≥13? | B. | i>14? | C. | i≥14? | D. | i≥15? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com