练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知直线过点，且与抛物线相交于两点，与轴交于点，其中点在第四象限，为坐标原点.

    (Ⅰ)当是中点时，求直线的方程；

    (Ⅱ)以为直径的圆交直线于点，求的值.

    【答案】（1）（2）4

    【解析】试题分析：（1）根据中点坐标公式得的横坐标，代入抛物线方程得的纵坐标，最后根据点斜式求直线的方程；（2）先设坐标,以及直线方程根据三点共线设为，由圆的性质得，并用坐标表示，联立直线方程与抛物线方程，利用韦达定理代入化简解得的值.

    试题解析：(Ⅰ)因为是中点，，点在轴上，

    所以的横坐标,代入得，，

    又点在第四象限，所以的坐标为，所以直线即直线的方程为.

    (Ⅱ)显然直线的斜率不为0，设直线的方程为,

    又三点共线，则可设为且，

    联立方程，化简得到,

    由韦达定理得,又在上，所以,

    因为在以为直径的圆上,所以，即,

    又，所以,即,

    所以.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】喜羊羊家族的四位成员与灰太狼、红太狼进行谈判，通过谈判他们握手言和，准备一起照合影像（排成一排）.

    （1）要求喜羊羊家族的四位成员必须相邻，有多少种排法？

    （2）要求灰太狼、红太狼不相邻，有多少种排法？

    （3）记灰太狼和红太狼之间的喜羊羊家族的成员个数为，求的概率分布表和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，在长方形中，为的中点，为线段上一动点．现将沿折起，形成四棱锥.

    （1）若与重合，且(如图2).证明：平面；

    （2）若不与重合，且平面平面 (如图3)，设，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四边形是直角梯形，，，且，是等边三角形，，为的中点．

    （1）求证：平面；

    （2）求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点是椭圆C：上的一点，椭圆C的离心率与双曲线的离心率互为倒数，斜率为直线l交椭圆C于B，D两点，且A、B、D三点互不重合．

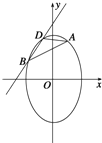
    （1）求椭圆C的方程；

    （2）若分别为直线AB，AD的斜率，求证：为定值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的中心在坐标原点，，是它的两个顶点，直线与直线相交于点，与椭圆相交于，两点．

    （Ⅰ）求椭圆的标准方程;

    （Ⅱ）若，求k的值；

    （Ⅲ）求四边形面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，点在以为焦点的双曲线上，过作轴的垂线，垂足为，若四边形为菱形，则该双曲线的离心率为（ ）

    A. B. 2 C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为、，直线：与椭圆相交于、两点，椭圆的上顶点与焦点关于直线对称，且．斜率为的直线与线段相交于点，与椭圆相交于、两点．

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）求四边形面积的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数, ．

    （Ⅰ）当x≥0时，f（x）≤h（x）恒成立，求a的取值范围；

    （Ⅱ）当x＜0时，研究函数F（x）=h（x）﹣g（x）的零点个数；

    （Ⅲ）求证：（参考数据：ln1.1≈0.0953）．

    查看答案和解析>>

    同步练习册答案