
【题目】如图,正方体![]() 中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN∥平面EFDB.
中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN∥平面EFDB.

科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 为椭圆
为椭圆![]() 上的动点,若
上的动点,若![]() 的最大值和最小值分别为
的最大值和最小值分别为![]() 和
和![]() .
.
(I)求椭圆![]() 的方程
的方程
(Ⅱ)设不过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,若直线
两点,若直线![]() 的斜率依次成等比数列,求
的斜率依次成等比数列,求![]() 面积的最大值
面积的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)对于实数![]() ,
,![]() ,若
,若![]() ,有
,有![]() ,求证:方程
,求证:方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
(2)若![]() ,函数
,函数![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值和最小值;
上的最大值和最小值;
(3)若存在实数![]() ,使得对于任意实数
,使得对于任意实数![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() +
+![]() =1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2
=1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的标准方程;
(2)过右焦点F2的直线l交椭圆于A,B两点,若y轴上一点M(0,![]() )满足|MA|=|MB|,求直线l的斜率k的值.
)满足|MA|=|MB|,求直线l的斜率k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P–ABCD中,ABCD是矩形,PA=AB,E为PB的中点.
(1)若过C,D,E的平面交PA于点F,求证:F为PA的中点;
(2)若平面PAB⊥平面PBC,求证:BC⊥PA.
查看答案和解析>>
科目:高中数学 来源: 题型:
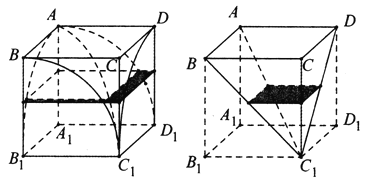
【题目】为推导球的体积公式,刘徽制造了一个牟合方盖(在一个正方体内作两个互相垂直的内切圆柱,这两个圆柱的公共部分叫做牟合方盖),但没有得到牟合方盖的体积.200年后,祖暅给出牟合方盖的体积计算方法,其核心过程被后人称为祖暅原理:缘幂势既同,则积不容异.意思是,夹在两个平行平面间的两个几何体被平行于这两个平行平面的任意平面所截,如果截面的面积总相等,那么这两个几何体的体积也相等.现在截取牟合方盖的八分之一,它的外切正方体![]() 的棱长为1,如图所示,根据以上信息,则该牟合方盖的体积为( )
的棱长为1,如图所示,根据以上信息,则该牟合方盖的体积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月22日,在韩国平昌冬奥会短道速滑男子![]() 米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子
米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子![]() 米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过
米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过![]() 个直道与弯道的交接口
个直道与弯道的交接口![]() .已知某男子速滑运动员顺利通过每个交接口的概率均为
.已知某男子速滑运动员顺利通过每个交接口的概率均为![]() ,摔倒的概率均为
,摔倒的概率均为![]() .假定运动员只有在摔倒或到达终点时才停止滑行,现在用
.假定运动员只有在摔倒或到达终点时才停止滑行,现在用![]() 表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.
表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.

(1)求该运动员停止滑行时恰好已顺利通过![]() 个交接口的概率;
个交接口的概率;
(2)求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com