
已知函数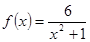
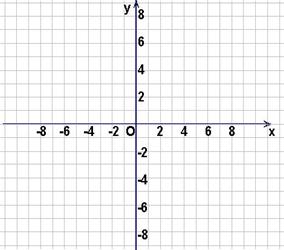
(1)在直角坐标系中,画出函数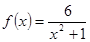 大致图像.
大致图像.
(2)关于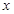 的不等式
的不等式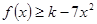 的解集一切实数,求实数
的解集一切实数,求实数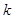 的取值范围;
的取值范围;
(1)略(2)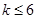
【解析】本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
(1)根据(2),定义域即看横轴覆盖部分,值域即看纵轴覆盖部分,奇偶性,看是否关于原点对称或关于纵轴对称.单调增区间看上升趋势,单调减区间看下降趋势,画出图象即可.
(2) 依题意,变形为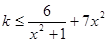 对一切实数
对一切实数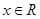 恒成立 ……6分
恒成立 ……6分
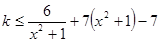 ,
,
设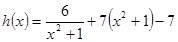 ,则
,则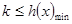 ,求解最值得到。
,求解最值得到。
解:
(1)图象特征大致如下,过点(0,6)定义域 的偶函数,
的偶函数,
值域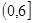 ,在
,在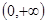 单调递减区间 ……4分
单调递减区间 ……4分
(2)解法一:依题意,变形为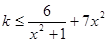 对一切实数
对一切实数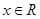 恒成立 ……6分
恒成立 ……6分
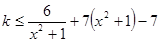 ,
,
设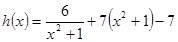 ,则
,则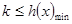 ……7分
……7分
因为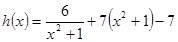 在
在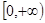 单调递减(可用函数单调性定义证明或导数证明或复合函数的单调性说明)(不说明单调性得1分,扣3分)
………11分
单调递减(可用函数单调性定义证明或导数证明或复合函数的单调性说明)(不说明单调性得1分,扣3分)
………11分
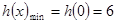
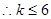 ………13分
………13分
解法二: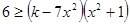 ,
,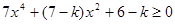 对一切实数恒成立
对一切实数恒成立
设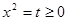 ,
,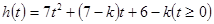 的最小值大于等于0恒成立;
的最小值大于等于0恒成立;
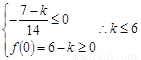
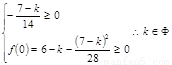


科目:高中数学 来源: 题型:
3
| ||
| 2 |
| 3 |
| 2 |
| ||
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.
如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.
| ||||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年莱西一中模拟)(12分)如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为![]() m,圆环的圆心距离地面的高度为
m,圆环的圆心距离地面的高度为![]() ,蚂蚁每分钟爬行一圈,若蚂蚁的起始位置在最低点P0处.
,蚂蚁每分钟爬行一圈,若蚂蚁的起始位置在最低点P0处.
(1)试确定在时刻t时蚂蚁距离地面的高度![]() ;
;
(2)画出函数![]() 在
在![]() 时的图象;
时的图象;
(3)在蚂蚁绕圆环爬行的一圈内,有多长时间蚂蚁距离地面超过![]() m?
m?

查看答案和解析>>
科目:高中数学 来源:2015届江苏省沭阳县高一下学期期中调研测试数学试卷(解析版) 题型:解答题
如图,某城市设立以城中心 为圆心、
为圆心、 公里为半径的圆形保护区,从保护区边缘起,在城中心
公里为半径的圆形保护区,从保护区边缘起,在城中心 正东方向上有一条高速公路
正东方向上有一条高速公路 、西南方向上有一条一级公路
、西南方向上有一条一级公路 ,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆
,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆 相切的直道
相切的直道 .已知通往一级公路的道路
.已知通往一级公路的道路 每公里造价为
每公里造价为 万元,通往高速公路的道路
万元,通往高速公路的道路 每公里造价是
每公里造价是 万元,其中
万元,其中 为常数,设
为常数,设 ,总造价为
,总造价为 万元.
万元.

(1)把 表示成
表示成 的函数
的函数 ,并求出定义域;
,并求出定义域;
(2)当 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低?
查看答案和解析>>
科目:高中数学 来源:1978年全国统一高考数学试卷(附加题)(解析版) 题型:解答题
 且倾斜角为30°的直线,圆C为圆心是坐标原点且半径等于1的圆,Q表示顶点在原点而焦点是
且倾斜角为30°的直线,圆C为圆心是坐标原点且半径等于1的圆,Q表示顶点在原点而焦点是 的抛物线,设A为L和C在第三象限的交点,B为C和Q在第四象限的交点.
的抛物线,设A为L和C在第三象限的交点,B为C和Q在第四象限的交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com