
分析 (1)当直线l的斜率k=-1时,直线l的方程为y-1=-(x-2),求出A,B的坐标,即可求△AOB的外接圆的面积;
(2)设直线l:y-1=k(x-2),求出A,B的坐标,表示面积,利用基本不等式,即可求出当△AOB的面积最小时,直线l的方程.
解答 解:当直线l的斜率k=-1时,直线l的方程为y-1=-(x-2),即x+y-3=0,可得A(3,0),B(0,3),|AB|=3$\sqrt{2}$,
且△AOB是直角三角形,AB为斜边,故△AOB的外接圆半径$r=\frac{{3\sqrt{2}}}{2}$…(4分)
所以外接圆的面积$s=π{({\frac{{3\sqrt{2}}}{2}})^2}=\frac{9π}{2}$…(5分)
(2)由题知直线l的斜率k存在,且k<0,设直线l:y-1=k(x-2),
令x=0,y=1-2k;令$y=0,x=2-\frac{1}{k}$,…(7分)
${S_{△AOB}}=\frac{1}{2}|{2-\frac{1}{k}}||{1-2k}|=\frac{1}{2}({\frac{1-2k}{-k}})({1-2k})=-\frac{1}{2}({\frac{1}{k}+4k-4})({k<0})$,
由勾函数知,当$k=-\frac{1}{2}$时,S△AOB最小…(9分)
故直线l的方程为$y-1=-\frac{1}{2}({x-2})$,即x+2y-4=0…(10分)
点评 本题考查圆的面积,考查直线方程,考查学生分析解决问题的能力,属于中档题.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 cm | B. | 8 cm | C. | 10 cm | D. | 12 cm |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
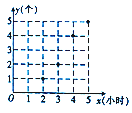 为确定加工某零件的时间,某工人做了四次实验,得到的数据的散点图如图所示.
为确定加工某零件的时间,某工人做了四次实验,得到的数据的散点图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com