
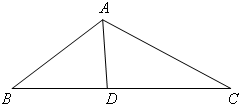
 满足一定条件的三角形如果周长和面积同时取得最小值(或最大值),则称此三角形为“周积三角形”.如图所示的△ABC满足∠BAC=120°,AD是∠BAC的平分线,且AD=1.设AB=x,AC=y.
满足一定条件的三角形如果周长和面积同时取得最小值(或最大值),则称此三角形为“周积三角形”.如图所示的△ABC满足∠BAC=120°,AD是∠BAC的平分线,且AD=1.设AB=x,AC=y.| xy |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| x-1 |
| xy |
| x2+y2+xy |
| (xy)2-xy |
| t2-t |
| 2t-2 | ||
2
|
| 3 |
| 1 |
| 2 |
| ||
| 4 |
| 3 |
| 3 |


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
| π |
| 2 |
| 1 |
| sina |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012年江苏省盐城中学高考数学二模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
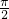 ),则aina+
),则aina+ 有最小值2
有最小值2 ,a=10,则满足条件的三角形只有一个.
,a=10,则满足条件的三角形只有一个.查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省成都市龙泉中学高一(下)期中数学试卷(解析版) 题型:填空题
 ),则aina+
),则aina+ 有最小值2
有最小值2 ,a=10,则满足条件的三角形只有一个.
,a=10,则满足条件的三角形只有一个.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com