
【题目】已知向量 ![]() ,
, ![]() ,设函数
,设函数 ![]() .
.
(1)求函数 ![]() 的单调递增区间;
的单调递增区间;
(2)在 ![]() 中,边
中,边 ![]() 分别是角
分别是角 ![]() 的对边,角
的对边,角 ![]() 为锐角,若
为锐角,若![]() ,
, ![]() ,
, ![]() 的面积为
的面积为 ![]() ,求边
,求边 ![]() 的长.
的长.
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】已知m、n、s、t∈R* , m+n=3, ![]() 其中m、n是常数且m<n,若s+t的最小值 是
其中m、n是常数且m<n,若s+t的最小值 是 ![]() ,满足条件的点(m,n)是椭圆
,满足条件的点(m,n)是椭圆 ![]() 一弦的中点,则此弦所在的直线方程为( )
一弦的中点,则此弦所在的直线方程为( )
A.x﹣2y+3=0
B.4x﹣2y﹣3=0
C.x+y﹣3=0
D.2x+y﹣4=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】咖啡馆配制两种饮料,甲种饮料每杯分别用奶粉、咖啡、糖9g、4g、3g;乙种饮料每杯分别用奶粉、咖啡、糖4g、5g、10g,已知每天使用原料限额为奶粉3600g,咖啡2000g,糖3000g,如果甲种饮料每杯能获利0.7元,乙种饮料每杯能获利1.2元,每天在原料使用的限额内,饮料能全部售完,问咖啡馆每天怎样安排配制饮料获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人. (Ⅰ)求该专业毕业总人数N和90~95分数段内的人数n;
(Ⅱ)现欲将90~95分数段内的n名人分配到几所学校,从中安排2人到甲学校去,若n人中仅有两名男生,求安排结果至少有一名男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为R,导函数f'(x)的图象如图所示,则函数f(x)( ) 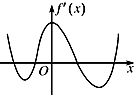
A.无极大值点,有四个极小值点
B.有三个极大值点,两个极小值点
C.有两个极大值点,两个极小值点
D.有四个极大值点,无极小值点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com