
【题目】在三棱柱![]() 中,底面是边长为4的等边三角形,侧棱垂直于底面,
中,底面是边长为4的等边三角形,侧棱垂直于底面,![]() ,M是棱AC的中点.
,M是棱AC的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】为监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取10个零件,度量其内径尺寸(单位:![]() ).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的内径尺寸服从正态分布
).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的内径尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记X表示某一天内抽取的10个零件中其内径尺寸在![]() 之外的零件数,求
之外的零件数,求![]() 及X的数学期望;
及X的数学期望;
(2)某天正常工作的一条生产线数据记录的茎叶图如下图所示:

①计算这一天平均值![]() 与标准差
与标准差![]() ;
;
②一家公司引进了一条这种生产线,为了检查这条生产线是否正常,用这条生产线试生产了5个零件,度量其内径分别为(单位:![]() ):95,103,109,112,119,试问此条生产线是否需要进一步调试,为什么?
):95,103,109,112,119,试问此条生产线是否需要进一步调试,为什么?
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑。若三棱锥P-ABC为鳖臑,PA⊥面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球的球面上,则球0的表面积为( )
A. 8πB. 12πC. 20πD. 24π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某度假酒店为了解会员对酒店的满意度,从中抽取50名会员进行调查,把会员对酒店的“住宿满意度”与“餐饮满意度”都分为五个评分标准:1分(很不满意);2分(不满意);3分(一般);4分(满意);5分(很满意).其统计结果如下表(住宿满意度为![]() ,餐饮满意度为
,餐饮满意度为![]() )
)
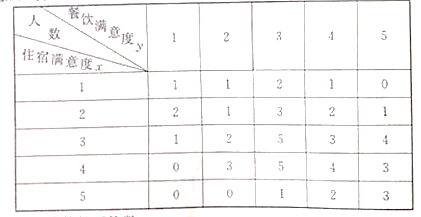
(1)求“住宿满意度”分数的平均数;
(2)求“住宿满意度”为3分时的5个“餐饮满意度”人数的方差;
(3)为提高对酒店的满意度,现从![]() 且
且![]() 的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为我国数学家赵爽(约3世纪初)在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则不同的涂色方案共有( )
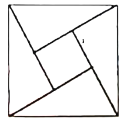
A.360种B.720种C.480种D.420种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国家积极推动美丽乡村建设的政策背景下,各地根据当地生态资源打造了众多特色纷呈的乡村旅游胜地.某人意图将自己位于乡村旅游胜地的房子改造成民宿用于出租,在旅游淡季随机选取100天,对当地已有的六间不同价位的民宿进行跟踪,统计其出租率![]() (
(![]() ),设民宿租金为
),设民宿租金为![]() (单位:元/日),得到如图所示的数据散点图.
(单位:元/日),得到如图所示的数据散点图.

(1)若用“出租率”近似估计旅游淡季民宿每天租出去的概率,求租金为388元的那间民宿在淡季内的三天中至少有2天闲置的概率.
(2)①根据散点图判断,![]() 与
与![]() 哪个更适合于此模型(给出判断即可,不必说明理由)?根据判断结果求回归方程;
哪个更适合于此模型(给出判断即可,不必说明理由)?根据判断结果求回归方程;
②若该地一年中旅游淡季约为280天,在此期间无论民宿是否出租,每天都要付出![]() 的固定成本,若民宿出租,则每天需要再付出
的固定成本,若民宿出租,则每天需要再付出![]() 的日常支出成本.试用①中模型进行分析,旅游淡季民宿租金约定为多少元时,该民宿在这280天的收益
的日常支出成本.试用①中模型进行分析,旅游淡季民宿租金约定为多少元时,该民宿在这280天的收益![]() 达到最大?
达到最大?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;![]() .
.
参考数据:记![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com