
【题目】设一组数据51,54,m,57,53的平均数是54,则这组数据的标准差等于 .
【答案】2
【解析】解:数据51,54,m,57,53的平均数是54,
即 ![]() ×(51+54+m+57+53)=54,
×(51+54+m+57+53)=54,
解得m=55,
所以这组数据的方差为
s2= ![]() ×[(51﹣54)2+(54﹣54)2+(55﹣54)2+(57﹣54)2+(53﹣54)2]=4,
×[(51﹣54)2+(54﹣54)2+(55﹣54)2+(57﹣54)2+(53﹣54)2]=4,
标准差为s=2.
所以答案是:2.
【考点精析】解答此题的关键在于理解平均数、中位数、众数的相关知识,掌握⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据.


科目:高中数学 来源: 题型:
【题目】如图,在三棱柱 ![]() 中,底面
中,底面 ![]() 是边长为2的等边三角形,
是边长为2的等边三角形, ![]() 为
为 ![]() 的中点.
的中点.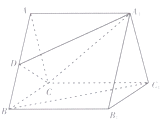
(1)求证: ![]() 平面
平面 ![]() ;
;
(2)若四边形 ![]() 是正方形,且
是正方形,且 ![]() , 求直线
, 求直线 ![]() 与平面
与平面 ![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标标系xoy中,已知曲线 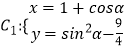 (α为参数,α∈R),在以原点O为极点,x轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线
(α为参数,α∈R),在以原点O为极点,x轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线 ![]() =
= ![]() ,曲线C3:ρ=2cosθ. (Ⅰ)求曲线C1与C2的交点M的直角坐标;
,曲线C3:ρ=2cosθ. (Ⅰ)求曲线C1与C2的交点M的直角坐标;
(Ⅱ)设A,B分别为曲线C2 , C3上的动点,求|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,F1、F2是双曲线 ![]() =1(a>0)的左、右焦点,过F1的直线l与双曲线交于点A、B,若△ABF2为等边三角形,则△BF1F2的面积为( )
=1(a>0)的左、右焦点,过F1的直线l与双曲线交于点A、B,若△ABF2为等边三角形,则△BF1F2的面积为( ) 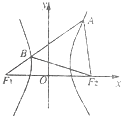
A.8
B.8 ![]()
C.8 ![]()
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】和谐高级中学共有学生570名,各班级人数如表:
一班 | 二班 | 三班 | 四班 | |
高一 | 52 | 51 | y | 48 |
高二 | 48 | x | 49 | 47 |
高三 | 44 | 47 | 46 | 43 |
已知在全校学生中随机抽取1名,抽到高二年级学生的概率是 ![]() .
.
(1)求x,y的值;
(2)现用分层抽样的方法在全校抽取114名学生,应分别在各年级抽取多少名?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆 ![]() 与圆
与圆 ![]() :
: ![]() 关于直线
关于直线 ![]() 对称,且点
对称,且点 ![]() 在圆
在圆 ![]() 上.
上.
(1)判断圆 ![]() 与圆
与圆 ![]() 的公切线的条数;
的公切线的条数;
(2)设 ![]() 为圆
为圆 ![]() 上任意一点,
上任意一点, ![]() ,
, ![]() ,
, ![]() 三点不共线,
三点不共线, ![]() 为
为 ![]() 的平分线,且交
的平分线,且交 ![]() 于
于 ![]() ,求证:
,求证: ![]() 与
与 ![]() 的面积之比为定值.
的面积之比为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,动点M到点F(1,0)的距离与它到直线x=2的距离之比为 ![]() . (Ⅰ)求动点M的轨迹E的方程;
. (Ⅰ)求动点M的轨迹E的方程;
(Ⅱ)设直线y=kx+m(m≠0)与曲线E交于A,B两点,与x轴、y轴分别交于C,D两点(且C,D在A,B之间或同时在A,B之外).问:是否存在定值k,对于满足条件的任意实数m,都有△OAC的面积与△OBD的面积相等,若存在,求k的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E,F分别为PC,BD的中点. 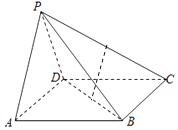
(1)证明:EF∥平面PAD;
(2)证明:直线PA⊥平面PCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com