
【题目】如图,正方形ADEF与梯形ABCD所在的平面互相垂直,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
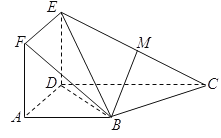
(1)求证:BM∥平面ADEF;
(2)求证:平面BDE⊥平面BEC.
【答案】(1)见解析;(2)见解析
【解析】
(1)取DE中点N,连接MN,AN,由三角形中位线定理得,四边形ABMN为平行四边形,即BM∥AN,再由线面平行的判定定理即可得到BM∥平面ADEF;
(2)由已知中正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,我们易得到ED⊥BC,解三角形BCD,可得BC⊥BD,由线面垂直的判定定理,可得BC⊥平面BDE,再由面面垂直的判定定理,即可得到平面BDE⊥平面BEC.
(1)取DE中点N,连接MN,AN,在△EDC中,M,N分别为EC,ED的中点
∴MN∥CD,且MN=![]() CD,由已知AB∥CD,AB=AD=2,CD=4,∴MN∥AB,且MN=AB
CD,由已知AB∥CD,AB=AD=2,CD=4,∴MN∥AB,且MN=AB
∴四边形ABMN为平行四边形,∴BM∥AN,又∵AN平面ADEF,BM平面ADEF,
∴BM∥平面ADEF.
(2)∵ADEF为正方形,∴ED⊥AD,又∵平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,且ED平面ADEF,
,且ED平面ADEF,
∴ED⊥平面ABCD,∴ED⊥BC,在直角梯形ABCD中,AB=AD=2,CD=4,可得BC=2![]() ,
,
在△BCD中,BD=BC=2![]() ,CD=4,∴BC⊥BD,∴BC⊥平面BDE,
,CD=4,∴BC⊥BD,∴BC⊥平面BDE,
又∵BC平面BEC,∴平面BDE⊥平面BEC


科目:高中数学 来源: 题型:
【题目】已知正方形的边长为4,E,F分别为![]() ,
,![]() 的中点,以
的中点,以![]() 为棱将正方形
为棱将正方形![]() 折成如图所示的
折成如图所示的![]() 的二面角,点M在线段
的二面角,点M在线段![]() 上.
上.
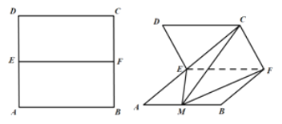
(1)若M为![]() 的中点,且直线
的中点,且直线![]() 与由A,D,E三点所确定平面的交点为G,试确定点G的位置,并证明直线
与由A,D,E三点所确定平面的交点为G,试确定点G的位置,并证明直线![]() 面
面![]() ;
;
(2)是否存在M,使得直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ;若存在,求此时
;若存在,求此时![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,连接椭圆四个顶点得到的菱形的面积为4.
,连接椭圆四个顶点得到的菱形的面积为4.
(1)求椭圆的方程;
(2)设![]() 是椭圆的右顶点,过点
是椭圆的右顶点,过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() 分别与椭圆交于
分别与椭圆交于![]() ,
,![]() 两点,求证:直线
两点,求证:直线![]() 过定点;
过定点;
(3)(只理科做)过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() ,
,![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 交椭圆于另一点
交椭圆于另一点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)当a≤0时,讨论函数f(x)的单调性;
(2)是否存在实数a,对任意的x1,x2![]() (0,+∞),且x1≠x2,都有
(0,+∞),且x1≠x2,都有![]() 恒成立.若存在,求出a的取值范围;若不存在,说明理由.
恒成立.若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() ).
).
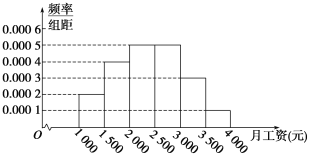
(1)求居民收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析,则月收入在![]() 的这段应抽取多少人?
的这段应抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 个编号为
个编号为![]() 、
、![]() 、
、![]() 、
、![]() 的不同小球全部放入
的不同小球全部放入![]() 个编号为
个编号为![]() 、
、![]() 、
、![]() 、
、![]() 的
的![]() 个不同盒子中.求:
个不同盒子中.求:
(1)每个盒至少一个球,有多少种不同的放法?
(2)恰好有一个空盒,有多少种不同的放法?
(3)每盒放一个球,并且恰好有一个球的编号与盒子的编号相同,有多少种不同的放法?
(4)把已知中![]() 个不同的小球换成四个完全相同的小球(无编号),其余条件不变,恰有一个空盒,有多少种不同的放法?
个不同的小球换成四个完全相同的小球(无编号),其余条件不变,恰有一个空盒,有多少种不同的放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,在点
,在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)已知![]() ,当
,当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)对于在![]() 中的任意一个常数
中的任意一个常数![]() ,是否存在正数
,是否存在正数![]() ,使得
,使得![]() ,请说明理由。
,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单调等比数列![]() ,首项为
,首项为![]() ,其前
,其前![]() 项和是
项和是![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差数列,数列
成等差数列,数列![]() 满足条件
满足条件![]()
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设![]() ,记数列
,记数列![]() 的前
的前![]() 项和是
项和是![]() .
.
①求![]() ;
;
②求正整数![]() ,使得对任意
,使得对任意![]() ,均有
,均有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成![]() 组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为
组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为![]() ,最右边一组的频数是
,最右边一组的频数是![]() .
.
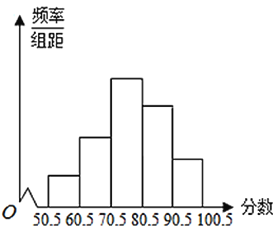
(1)成绩落在哪个范围的人数最多?并求出该小组的频数、频率;
(2)估计这次竞赛中,成绩高于![]() 分的学生占总人数的百分百.
分的学生占总人数的百分百.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com