
【题目】对于定义在![]() 上的函数
上的函数![]() ,若函数
,若函数![]() 满足:①在区间
满足:①在区间![]() 上单调递减,②存在常数
上单调递减,②存在常数![]() ,使其值域为
,使其值域为![]() ,则称函数
,则称函数![]() 是函数
是函数![]() 的“渐近函数”.
的“渐近函数”.
(1)判断函数![]() 是不是函数
是不是函数![]() 的“渐近函数”,说明理由;
的“渐近函数”,说明理由;
(2)求证:函数![]() 不是函数
不是函数![]() 的“渐近函数”;
的“渐近函数”;
(3)若函数![]() ,
,![]() ,求证:当且仅当
,求证:当且仅当![]() 时,
时,![]() 是
是![]() 的“渐近函数”.
的“渐近函数”.
【答案】(1)是,见解析;(2)见解析;(3)见解析
【解析】
(1)用反比例型函数的单调性,可以判断函数![]() 是否满足定义中的两条性质,进而可以判断出函数
是否满足定义中的两条性质,进而可以判断出函数![]() 是不是函数
是不是函数![]() 的“渐近函数”.
的“渐近函数”.
(2)利用指数型函数的单调性、单调性的性质,证明出函数![]() 至少不满足定义中两条性质中的一条,即可证明出函数
至少不满足定义中两条性质中的一条,即可证明出函数![]() 不是函数
不是函数![]() 的“渐近函数”;
的“渐近函数”;
(3)根据定义可知函数![]() 是
是![]() 上的减函数.这样运用单调性的定义,可以求出
上的减函数.这样运用单调性的定义,可以求出![]() 的取值范围,再根据定义中的第二条性质再求出
的取值范围,再根据定义中的第二条性质再求出![]() 的取值范围,最后可以确定
的取值范围,最后可以确定![]() 的值.
的值.
(1) 函数![]() 是函数
是函数![]() 的“渐近函数”理由如下:
的“渐近函数”理由如下:
![]() ,
,
显然函数在![]() 上单调递减,当
上单调递减,当![]() 时,
时, ![]() ,因此存在常数
,因此存在常数![]() ,使得函数
,使得函数![]() 的值域为
的值域为![]() ,故函数
,故函数![]() 是函数
是函数![]() 的“渐近函数”;
的“渐近函数”;
(2) ![]() ,由指数型复合函数的单调性和函数单调性的性质可知:函数
,由指数型复合函数的单调性和函数单调性的性质可知:函数![]() 在
在![]() 上单调递减,符合定义中的第一条性质,
上单调递减,符合定义中的第一条性质,
当![]() 时,
时, ![]() ,
,![]() ,故函数
,故函数![]() 的值趋近负无穷大,故不满足第二条性质,故函数
的值趋近负无穷大,故不满足第二条性质,故函数![]() 不是函数
不是函数![]() 的“渐近函数”;
的“渐近函数”;
(3) 由题意可知:![]() 在
在![]() 上是减函数.
上是减函数.
设![]() 且
且![]() ,则有
,则有
![]() ,
,
因为![]() 且
且![]() ,所以
,所以![]() ,
,
因为![]() 在
在![]() 上是减函数,而
上是减函数,而![]() ,则必有
,则必有
![]() ,所以
,所以![]() ,即
,即![]() ;
;
函数![]() 在
在![]() 上的值域为
上的值域为![]() ,则有
,则有![]() ,
,
显然![]() ,当
,当![]() 时,
时,![]() ,因此
,因此![]() ,综上所述:
,综上所述:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在直角坐标![]() 中,设椭圆
中,设椭圆![]() :
:![]() 的左右两个焦点分别为
的左右两个焦点分别为![]() ,
,![]() ,过右焦点
,过右焦点![]() 且与
且与![]() 轴垂直的直线
轴垂直的直线![]() 与椭圆
与椭圆![]() 相交,其中一个交点为
相交,其中一个交点为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() ,
,![]() 经过点
经过点![]() 且斜率为
且斜率为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 有两个不同的
有两个不同的![]() 和
和![]() 交点,请问是否存在常数
交点,请问是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求出
共线?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四种说法:①函数![]() 的单调递增区间是
的单调递增区间是![]() ;②函数
;②函数![]() 与
与![]() 的值域相同;③函数
的值域相同;③函数![]() 与
与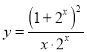 均是奇函数;④若函数
均是奇函数;④若函数![]() 在
在![]() 上有零点,则实数
上有零点,则实数![]() 的取值范围是
的取值范围是![]() .其中正确结论的序号是_______.
.其中正确结论的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哈三中群力校区高二、六班同学用随机抽样的办法对所在校区老师的饮食习惯进行了一次调查, 饮食指数结果用茎叶图表示如图, 图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.

(1)完成下列![]() 列联表:
列联表:

能否有![]() 的把握认为老师的饮食习惯与年龄有关?
的把握认为老师的饮食习惯与年龄有关?
(2)从调查的结果中饮食指数在![]() 的老师内任选3名老师, 设“选到的三位老师饮食指数之和不超过105”为事件
的老师内任选3名老师, 设“选到的三位老师饮食指数之和不超过105”为事件![]() , 求事件
, 求事件![]() 发生的概率;
发生的概率;
(3)为了给食堂提供老师的饮食信息, 根据(1)的结论,能否有更好的抽样方法来估计老师的饮食习惯, 并说明理由.
附:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某地区乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
时间代号 | 1 | 2 | 3 | 4 | 5 | 6 |
储蓄存款 | 3.5 | 5 | 6 | 7 | 8 | 9.5 |
(1)求关于![]() 的回归方程
的回归方程![]() ,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
(2)在含有一个解释变量的线性模型中,![]() 恰好等于相关系数
恰好等于相关系数![]() 的平方,当
的平方,当![]() 时,认为线性回归模型是有效的,请计算
时,认为线性回归模型是有效的,请计算![]() 并且评价模型的拟合效果(计算结果精确到
并且评价模型的拟合效果(计算结果精确到![]() ).
).
附:
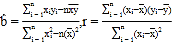 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() 过
过![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() (
(![]() 在第二象限).
在第二象限).
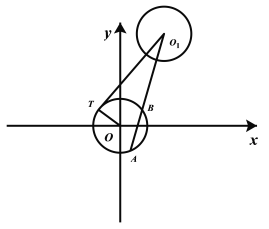
(1)求![]() 的正弦值;
的正弦值;
(2)已知点![]() ,过
,过![]() 点分别作两圆切线,若切线长相等,求
点分别作两圆切线,若切线长相等,求![]() 关系;
关系;
(3)是否存在定点![]() ,使过点
,使过点![]() 有无数对相互垂直的直线
有无数对相互垂直的直线![]() 满足
满足![]() ,且它们分别被圆
,且它们分别被圆![]() 、圆
、圆![]() 所截得的弦长相等?若存在,求出所有的点
所截得的弦长相等?若存在,求出所有的点![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com