
【题目】将函数f(x)=sin2x的图象向右平移φ(0<φ< ![]() )个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min=
)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min= ![]() ,则φ=( )
,则φ=( )
A.![]()
B.![]()
C.![]()
D.![]()
科目:高中数学 来源: 题型:
【题目】已知命题p:对数![]() 有意义;命题q:实数t满足不等式
有意义;命题q:实数t满足不等式![]() .
.
(Ⅰ)若命题p为真,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若命题p是命题q的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :若关于
:若关于![]() 的方程
的方程![]() 无实数根,则
无实数根,则![]() ;命题
;命题![]() :若关于
:若关于![]() 的方程
的方程![]() 有两个不相等的正实数根,则
有两个不相等的正实数根,则![]() .
.
(1)写出命题![]() 的否命题,并判断命题
的否命题,并判断命题![]() 的真假;
的真假;
(2)判断命题“![]() 且
且![]() ”的真假,并说明理由.
”的真假,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图所示的程序框图,解答下列问题:
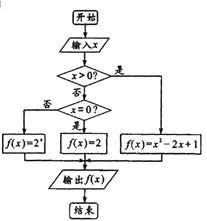
(1)求输入的![]() 的值分别为
的值分别为![]() 时,输出的
时,输出的![]() 的值;
的值;
(2)根据程序框图,写出函数![]() (
(![]() )的解析式;并求当关于
)的解析式;并求当关于![]() 的方程
的方程![]() 有三个互不相等的实数解时,实数
有三个互不相等的实数解时,实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一网站营销部为统计某市网友2017年12月12日在某网店的网购情况,随机抽查了该市60名网友在该网店的网购金额情况,如下表:
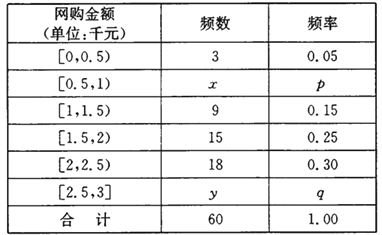
若将当日网购金额不小于2千元的网友称为“网购达人”,网购金额小于2千元的网友称为“网购探者”.已知“网购达人”与“网购探者”人数的比例为2:3.
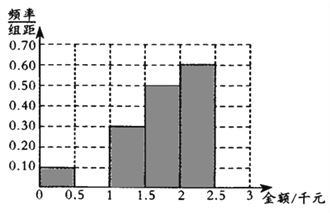
(1)确定![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数;若平均数和中位数至少有一个不低于2千元,则该网店当日被评为“皇冠店”,试判断该网店当日能否被评为“皇冠店”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张师傅欲将一球形的石材工件削砍加工成一圆柱形的新工件,已知原球形工件的半径为![]() ,则张师傅的材料利用率的最大值等于(注:材料利用率=
,则张师傅的材料利用率的最大值等于(注:材料利用率=![]() )( )
)( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】设球半径为R,圆柱的体积为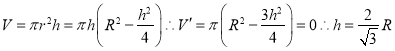 时圆柱的体积最大为
时圆柱的体积最大为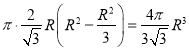 ,因此材料利用率=
,因此材料利用率=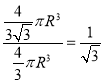 ,选C.
,选C.
点睛:空间几何体与球接、切问题的求解方法
求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.
【题型】单选题
【结束】
12
【题目】已知抛物线![]() :
: ![]()
![]() 在点
在点![]() 处的切线与曲线
处的切线与曲线![]() :
: ![]() 相切,若动直线
相切,若动直线![]() 分别与曲线
分别与曲线![]() 、
、![]() 相交于
相交于![]() 、
、![]() 两点,则
两点,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com