
【题目】如图,△ABC是边长为4的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=2.
(1)求证:AD⊥BE
(2)求平面AEC和平面BDE所成锐二面角的余弦值.
【答案】
(1)解:以OA,OC,OD为x,y,z的正方向建立直角坐标系,
则有: ![]()
![]()
由于 ![]() ,
,
故AD⊥BE.
(2)解:如图建立坐标系,

则 ![]() ,
,
![]() ,
,
设平面AEC的法向量为 ![]() ,
,
则  所以
所以 ![]() ,
,
令y1=1,则 ![]()
所以 ![]() ,
,
设平面BDE的法向量为 ![]()
则 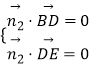 所以
所以 ![]() ,令x2=1,则y2=0,z1=﹣1
,令x2=1,则y2=0,z1=﹣1
所以 ![]() ,
,
所以  .
.
【解析】(1)建立空间坐标系,求出点的坐标,利用向量法证明直线垂直.(2)求出平面的法向量,利用向量法进行求解即可.
【考点精析】根据题目的已知条件,利用空间中直线与直线之间的位置关系的相关知识可以得到问题的答案,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


科目:高中数学 来源: 题型:
【题目】设数列{an}是各项均为正数的等比数列,且a1=3,a2+a3=36.
(1)求数列{an}的通项公式;
(2)若数列{bn}对任意的正整数n都有 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() =2n+1,求b1+b2+b3+…+b2015的值.
=2n+1,求b1+b2+b3+…+b2015的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,且Sn=4an﹣p,其中p是不为零的常数.
(1)证明:数列{an}是等比数列;
(2)当p=3时,若数列{bn}满足bn+1=bn+an(n∈N*),b1=2,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,AB,BC,BD两两垂直,BC=BD=2,点E是CD的中点,异面直线AD与BE所成角的余弦值为![]() ,则直线BE与平面ACD所成角的正弦值为( )
,则直线BE与平面ACD所成角的正弦值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量 ![]() =(a,
=(a, ![]() b)与
b)与 ![]() =(cosA,sinB)平行.
=(cosA,sinB)平行.
(1)求A;
(2)若a= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型工厂安排甲、乙两种产品的生产,已知工厂生产甲、乙两种产品每吨所需要的原材料A,B,C的数量和一周内可用资源数量如下表所示:
原材料 | 甲(吨) | 乙(吨) | 资源数量(吨) |
A | 1 | 1 | 50 |
B | 4 | 0 | 160 |
C | 2 | 5 | 200 |
如果甲产品每吨的利润为300元,乙产品每吨的利润为200元,那么适当安排生产后,工厂每周可获得的最大利润为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为  (t为参数),曲线C的极坐标方程是ρcos2θ=sinθ,以极点为原点,极轴为x轴正方向建立直角坐标系,点M(﹣1,0),直线l与曲线C交于A、B两点.
(t为参数),曲线C的极坐标方程是ρcos2θ=sinθ,以极点为原点,极轴为x轴正方向建立直角坐标系,点M(﹣1,0),直线l与曲线C交于A、B两点.
(1)写出直线l的极坐标方程与曲线C普通方程;
(2)线段MA,MB长度分别记为|MA|,|MB|,求|MA||MB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为  (t为参数),在以坐标原点O为极点,x轴的正非负半轴为极轴,取相同单位长度的极坐标系中,圆的极坐标方程为ρ=4sinθ.
(t为参数),在以坐标原点O为极点,x轴的正非负半轴为极轴,取相同单位长度的极坐标系中,圆的极坐标方程为ρ=4sinθ.
(1)求直线l被圆截得的弦长;
(2)从极点作圆C的弦,求各弦中点的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com