
【题目】设函数![]() ,
,![]() ,
,![]() ,其中
,其中![]() 是
是![]() 的导函数.
的导函数.
(1)令![]() ,
,![]() ,
,![]() ,求
,求![]() 的表达式;
的表达式;
(2)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)求出![]() 的解析式,依次计算即可得出猜想;
的解析式,依次计算即可得出猜想;
(2)已知![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
设![]() (x≥0),
(x≥0),
则φ′(x)=![]() =-
=-![]() =
=![]() ,
,
对![]() 进行讨论,求出
进行讨论,求出![]() 的最小值,令
的最小值,令![]() 恒成立即可;
恒成立即可;
详解:
由题设得,g(x)=![]() (x≥0).
(x≥0).
(1)由已知,g1(x)=![]() ,
,
g2(x)=g(g1(x))=![]() =
=![]() ,
,
g3(x)=![]() ,…,可得gn(x)=
,…,可得gn(x)=![]() .
.
下面用数学归纳法证明.
①当n=1时,g1(x)=![]() ,结论成立.
,结论成立.
②假设n=k时结论成立,即gk(x)=![]() .
.
那么,当n=k+1时,
gk+1(x)=g(gk(x))=![]() =
=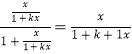 ,
,
即结论成立.
由①②可知, 结论对n∈N+成立.
所以gn(x)=![]() .
.
(2)已知f(x)≥ag(x)恒成立,即ln(1+x)≥![]() 恒成立.
恒成立.
设φ(x)=ln(1+x)-![]() (x≥0),
(x≥0),
则φ′(x)=![]() =-
=-![]() =
=![]() ,
,
当a≤1时,φ′(x)≥0(仅当x=0,a=1时等号成立),
∴φ(x)在[0,+∞)上单调递增,又φ(0)=0,
∴φ(x)≥0在[0,+∞)上恒成立,
∴a≤1时,ln(1+x)≥![]() 恒成立(仅当x=0时等号成立).
恒成立(仅当x=0时等号成立).
当a>1时,对x∈(0,a-1]有φ′(x)<0,∴φ(x)在(0,a-1]上单调递减,
∴φ(a-1)<φ(0)=0,
即a>1时,存在x>0,使φ(x)<0,故知ln(1+x)≥![]() 不恒成立.
不恒成立.
综上可知,a的取值范围是(-∞,1].


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某工厂今年1月、2月、3月生产某产品分别为1万件、1.2万件、1.3万件,为了估计以后每月的产量,以这三个月的产量为依据,用一个函数模拟该产品的月产量,![]() 与月份
与月份![]() 的关系,模拟函数可以选用二次函数或函数
的关系,模拟函数可以选用二次函数或函数![]() 、
、![]() 、
、![]() 为常数)已知四月份该产品的产量为1.37万件,请问用以上哪个函数作模拟函数较好?说明理由.
为常数)已知四月份该产品的产量为1.37万件,请问用以上哪个函数作模拟函数较好?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 是经过小城
是经过小城![]() 的东西方向与南北方向的两条公路,小城
的东西方向与南北方向的两条公路,小城![]() 位于小城
位于小城![]() 的东北方向,直线距离
的东北方向,直线距离![]() .现规划经过小城
.现规划经过小城![]() 修建公路
修建公路![]() (
(![]() ,
,![]() 分别在
分别在![]() 与
与![]() 上),与
上),与![]() ,
,![]() 围成三角形区域
围成三角形区域![]() .
.
(1)设![]() ,
,![]() ,求三角形区域
,求三角形区域![]() 周长的函数解析式
周长的函数解析式![]() ;
;
(2)现计划开发周长最短的三角形区域![]() ,求该开发区域的面积.
,求该开发区域的面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的分类垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1 000吨生活垃圾,数据统计如下(单位:吨):
“厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
(1)试估计厨余垃圾投放正确的概率P;
(2)试估计生活垃圾投放错误的概率;
(3)假设厨余垃圾在“厨余垃圾”箱,“可回收物”箱,“其他垃圾”箱的投放量分别为a、b、c,其中a>0,a+b+c=600. 当数据a、b、c的方差s2最大时,写出a、b、c的值(结论不要求证明),并求出此时s2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系xOy中,过点P(﹣1,﹣2)的直线l的参数方程为 ![]() (t为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsinθtanθ=2a(a>0),直线l与曲线C相交于不同的两点M、N.
(t为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsinθtanθ=2a(a>0),直线l与曲线C相交于不同的两点M、N.
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若|PM|=|MN|,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x+alnx(a>0).
(Ⅰ)当a=2时,试求函数图线过点(1,f(1))的切线方程;
(Ⅱ)当a=1时,若关于x的方程f(x)=x+b有唯一实数解,试求实数b的取值范围;
(Ⅲ)若函数f(x)有两个极值点x1、x2(x1<x2),且不等式f(x1)≥mx2恒成立,试求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是异面直线,则以下四个命题:①存在分别经过直线
是异面直线,则以下四个命题:①存在分别经过直线![]() 和
和![]() 的两个互相垂直的平面;②存在分别经过直线
的两个互相垂直的平面;②存在分别经过直线![]() 和
和![]() 的两个平行平面;③经过直线
的两个平行平面;③经过直线![]() 有且只有一个平面垂直于直线
有且只有一个平面垂直于直线![]() ;④经过直线
;④经过直线![]() 有且只有一个平面平行于直线
有且只有一个平面平行于直线![]() ,其中正确的个数有( )
,其中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为选派一名学生参加全市实践活动技能竟赛,A、B两位同学在学校的学习基地现场进行加工直径为20mm的零件测试,他俩各加工的10个零件直径的相关数据如图所示(单位:mm)

A、B两位同学各加工的10个零件直径的平均数与方差列于下表;
平均数 | 方差 | |
A | 20 | 0.016 |
B | 20 | s2B |
根据测试得到的有关数据,试解答下列问题:
(Ⅰ)计算s2B,考虑平均数与方差,说明谁的成绩好些;
(Ⅱ)考虑图中折线走势情况,你认为派谁去参赛较合适?请说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
直线![]() 的参数方程为
的参数方程为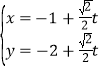 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)已知![]() ,设点
,设点![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com