
【题目】某家电公司进行关于消费档次的调查,根据家庭年均家电消费额将消费档次分为4组:不超过3000元、超过3000元且不超过5000元、超过5000元且不超过10000元、超过10000元,从A、B两市中各随机抽取100个家庭,统计数据如下表所示:
消费 档次 | 不超过3000元 | 超过3000元 且不超过5000元 | 超过5000元 且不超过10000元 | 超过10000元 |
A市 | 20 | 50 | 20 | 10 |
B市 | 50 | 30 | 10 | 10 |
年均家电消费额不超过5000元的家庭视为中低消费家庭,超过5000元的视为中高消费家庭.
(1)从A市的100个样本中任选一个家庭,求此家庭属于中低消费家庭的概率;
(2)现从A、B两市中各任选一个家庭,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
(3)以各消费档次的区间中点对应的数值为该档次的家庭年均家电消费额,估计A、B两市中,哪个市的家庭年均家电消费额的方差较大(直接写出结果,不必说明理由).
【答案】(1)![]() (2)
(2)![]() (3)B市的家庭年均家电消费额的方差较大
(3)B市的家庭年均家电消费额的方差较大
【解析】
(1)由古典概型概率公式可直接求得结果;
(2)根据积事件概率公式和分类加法原理可计算得到概率;
(3)根据数据的分散程度可确定结果.
(1)![]() 市的
市的![]() 个样本中有
个样本中有![]() 个中低消费家庭,
个中低消费家庭,
则从![]() 市的
市的![]() 个样本中任选一个家庭,此家庭属于中低消费家庭的概率
个样本中任选一个家庭,此家庭属于中低消费家庭的概率![]() .
.
(2)从![]() 市的
市的![]() 个样本中选一个家庭,记为
个样本中选一个家庭,记为![]() ;从
;从![]() 市的
市的![]() 个样本中选一个家庭,记为
个样本中选一个家庭,记为![]() ,设
,设![]() 的消费档次不低于
的消费档次不低于![]() 的消费档次为事件
的消费档次为事件![]() ,
,
则![]() ,
,
![]() 估计甲的消费档次不低于乙的消费档次的概率约为
估计甲的消费档次不低于乙的消费档次的概率约为![]() .
.
(3)![]() 市的家庭年均家电消费额的方差较大.
市的家庭年均家电消费额的方差较大.
理由如下:从表中数据可知,在![]() 市的100个样本与
市的100个样本与![]() 市的
市的![]() 个样本中,
个样本中,![]() 市的样本分布较为分散,所以
市的样本分布较为分散,所以![]() 市的家庭年均家电消费额的方差较大.
市的家庭年均家电消费额的方差较大.


科目:高中数学 来源: 题型:
【题目】2018年,南昌市召开了全球VR产业大会,为了增强对青少年VR知识的普及,某中学举行了一次普及VR知识讲座,并从参加讲座的男生中随机抽取了50人,女生中随机抽取了70人参加VR知识测试,成绩分成优秀和非优秀两类,统计两类成绩人数得到如下的列联表:
优秀 | 非优秀 | 总计 | |
男生 | a | 35 | 50 |
女生 | 30 | d | 70 |
总计 | 45 | 75 | 120 |
(1)确定a,d的值;
(2)试判断能否有90%的把握认为VR知识的测试成绩优秀与否与性别有关;
(3)为了宣传普及VR知识,从该校测试成绩获得优秀的同学中按性别采用分层抽样的方法,随机选出6名组成宣传普及小组.现从这6人中随机抽取2名到校外宣传,求“到校外宣传的2名同学中至少有1名是男生”的概率.
附:![]()
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,E是AD的中点,O是AC与BE的交点.将
,E是AD的中点,O是AC与BE的交点.将![]() 沿BE折起到图2中
沿BE折起到图2中![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() .
.
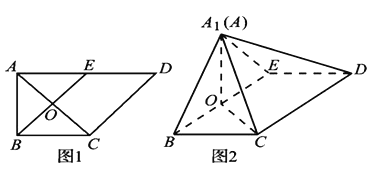
(1)证明:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求平面
,求平面![]() 与平面
与平面![]() 夹角(锐角)的余弦值.
夹角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有若干扑克牌:6张牌面分别是2,3,4,5,6,7的扑克牌各一张,先后从中取出两张.若每次取后放回,连续取两次,点数之和是偶数的概率为![]() ;若每次取后不放回,连续取两次,点数之和是偶数的概率为
;若每次取后不放回,连续取两次,点数之和是偶数的概率为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.以上三种情况都有可能
D.以上三种情况都有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位生物学专家在筛选临床抗病毒药物![]() ,
,![]() ,
,![]() ,
,![]() 时做出如下预测:
时做出如下预测:
甲说:![]() 和
和![]() 都有效;
都有效;
乙说:![]() 和
和![]() 不可能同时有效;
不可能同时有效;
丙说:![]() 有效;
有效;
丁说:![]() 和
和![]() 至少有一种有效.
至少有一种有效.
临床试验后证明,有且只有两种药物有效,且有且只有两位专家的预测是正确的,由此可判断有效的药物是( )
A.![]() 和
和![]() B.
B.![]() 和
和![]() C.
C.![]() 和
和![]() D.
D.![]() 和
和![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①![]() 中,
中,![]() 是
是![]() 成立的充要条件;
成立的充要条件;
②当![]() 时,有
时,有![]() ;
;
③已知![]() 是等差数列
是等差数列![]() 的前n项和,若
的前n项和,若![]() ,则
,则![]() ;
;
④若函数![]() 为
为![]() 上的奇函数,则函数
上的奇函数,则函数![]() 的图象一定关于点
的图象一定关于点![]() 成中心对称.其中所有正确命题的序号为___________.
成中心对称.其中所有正确命题的序号为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的发展理念,贵阳一中“保护饮用水源地”课题研究小组的同学们对红枫湖、百花湖、阿哈水库、花溪水库、北郊水库5处水源地进行了样本采集并送环保部门进行水质检测.已知5处水源地中有1处被某污染物污染,需要通过检测水源样本来确定被污染的水源地现有三个检測方案:
方案甲:对5个样本逐个检测,直到能确定被污染的水源地为止.
方案乙:先任取1个样本进行检测,若检测到污染物,则检测结束;若未检测到污染物,则在剩余4个样本中任取2个,并将这2个样本取部分混合在一起检测,若检测到污染物,则再在这2个样本中任取一个检测,否则在剩余2个未检测样本中任取一个检测.
方案丙:先任取2个样本,并将这2个样本取部分混合在一起检测,若检测到污染物,则再在这2个样本中任取一个检测;若未检测到污染物,则对剩余3个未检测样本进行逐个检测,直到能确定被污染的水源地为止.假设随机变量![]() 分别表示用方案甲、方案乙、方案丙进行检测所需的检测次数.
分别表示用方案甲、方案乙、方案丙进行检测所需的检测次数.
(1)求![]() 能取到的最大值和其对应的概率;
能取到的最大值和其对应的概率;
(2)求![]() 的期望假设每次检测的费用都相同,请从经济角度说明方案乙和方案丙哪一个更适合?
的期望假设每次检测的费用都相同,请从经济角度说明方案乙和方案丙哪一个更适合?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com