
分析 圆的方程化为标准方程,求出圆心和半径,过定点A(1,2)作圆的切线有两条,点A必在圆外,推出不等式,然后解答不等式即可.
解答 解:将圆的方程配方得(x+$\frac{a}{2}$)2+(y+1)2=$\frac{4-3{a}^{2}}{4}$,圆心C的坐标为(-$\frac{a}{2}$,-1),半径r=$\sqrt{\frac{4-3{a}^{2}}{4}}$,
条件是4-3a2>0,过点A(1,2)所作圆的切线有两条,则点A必在圆外,即$\sqrt{(1+\frac{a}{2})^{2}+(2+1)^{2}}$>$\sqrt{\frac{4-3{a}^{2}}{4}}$.
化简得a2+a+9>0.
由4-3a2>0,a2+a+9>0,
解之得-$\frac{2\sqrt{3}}{3}$<a<$\frac{2\sqrt{3}}{3}$,a∈R.
故a的取值范围是(-$\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$).
点评 本题考查圆的切线方程,直线和圆的方程的应用,考查一元二次不等式的解法,逻辑思维能力,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
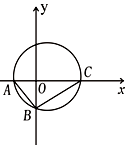 如图所示,在Rt△ABC中,已知A(-2,0),直角顶点$B(0,-2\sqrt{2})$,点C在x轴上.
如图所示,在Rt△ABC中,已知A(-2,0),直角顶点$B(0,-2\sqrt{2})$,点C在x轴上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
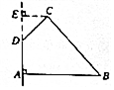 如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,则四边形ABCD绕AD旋转一周所成几何体的表面积为( )
如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,则四边形ABCD绕AD旋转一周所成几何体的表面积为( )| A. | (60+4$\sqrt{2}$)π | B. | (60+8$\sqrt{2}$)π | C. | (56+8$\sqrt{2}$)π | D. | (56+4$\sqrt{2}$)π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①②④ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com