
【题目】已知a≤8.函数f(x)=a1nx﹣x2+5,g(x)=2x+![]()
(1)若f(x)的极大值为5,求a的值
(2)若关于x的不等式f(x)≤g(x)在区间[1,+∞)上恒成立,求a的取值范围,(1n2≈0.7)
【答案】(1)a=2e;(2)![]()
【解析】
(1)求导后分![]() 的不同取值范围求
的不同取值范围求![]() 的最值,进而分析函数的极值再代入求解即可.
的最值,进而分析函数的极值再代入求解即可.
(2)构造函数![]() 再求导分析单调性,分情况讨论最大值再根据最大值
再求导分析单调性,分情况讨论最大值再根据最大值![]() 求关于参数a的取值范围即可.
求关于参数a的取值范围即可.
(1)函数f(x)=a1nx﹣x2+5,函数的定义域为{x|x>0},
函数的f(x)的导数f′(x)=![]() ﹣2x=
﹣2x=![]() ,
,
当a≤0,则f′(x)<0,此时函数单调递减无极大值,∴a>0,
∴f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上函数单调递减,
,+∞)上函数单调递减,
函数f(x)的极大值为:f(![]() )=5,解得:a=2e;
)=5,解得:a=2e;
(2)关于x的不等式f(x)≤g(x)在区间[1,+∞)上恒成立,
即:a1nx﹣x2+5﹣2x﹣![]() ≤0在区间[1,+∞)上恒成立,
≤0在区间[1,+∞)上恒成立,
令为h(x)=a1nx﹣x2+5﹣2x﹣![]() ,x∈[1,+∞),
,x∈[1,+∞),
则有:h′(x)=![]() ﹣2x﹣2+
﹣2x﹣2+![]() =﹣
=﹣![]() ,
,
①当a≤2时,h′(x)≤0,h(x)在区间[1,+∞)上单调递减,
h(x)最大值=h(1)=2﹣a≤0,即:a≥2,∴a=2;
②当a>2时,h(x)在区间[1,![]() )上单调递增,在区间(
)上单调递增,在区间(![]() ,+∞)上单调递减,
,+∞)上单调递减,
h(x)最大值=h(![]() )=
)=![]() 1n
1n![]() ﹣
﹣![]() +5﹣2
+5﹣2![]() ≤0,
≤0,
令![]() =t∈(1,4],即:t1nt﹣t+5﹣4
=t∈(1,4],即:t1nt﹣t+5﹣4![]() ≤0,令u(t)=t1nt﹣t+5﹣4
≤0,令u(t)=t1nt﹣t+5﹣4![]() ,u′(t)=1nt﹣
,u′(t)=1nt﹣![]() ,
,
由u(t)在(1,4]上单调递增,且u′(1)<0,u′(4)>0,
知存在t0∈(1,4]使得且u′(t0)=0,
u(t)在区间(1,t0)上单调递减,在区间(t0,4]上单调递增,
又且u(1)=0,u(4)=41n4﹣7=8ln2﹣7<0,
∴t1nt﹣t+5﹣4![]() ≤0,在t∈(1,4]上恒成立,∵已知a≤8,故:2<a≤8,
≤0,在t∈(1,4]上恒成立,∵已知a≤8,故:2<a≤8,
即a的取值范围是:a∈![]()


科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() .
.
(1)求椭圆C的离心率;
(2)设![]() 分别为椭圆C的左右顶点,点P在椭圆C上,直线AP,BP分别与直线
分别为椭圆C的左右顶点,点P在椭圆C上,直线AP,BP分别与直线![]() 相交于点M,N.当点P运动时,以M,N为直径的圆是否经过
相交于点M,N.当点P运动时,以M,N为直径的圆是否经过![]() 轴上的定点?试证明你的结论.
轴上的定点?试证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴.为迎接2014年“双十一”网购狂欢节,某厂家拟投入适当的广告费,对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量p万件与促销费用x万元满足![]() (其中
(其中![]() ,a为正常数).已知生产该产品还需投入成本
,a为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为
![]() 元/件,假定厂家的生产能力完全能满足市场的销售需求.
元/件,假定厂家的生产能力完全能满足市场的销售需求.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 与
与![]() 的交点坐标;
的交点坐标;
(2)过曲线![]() 上任一点
上任一点![]() 作与
作与![]() 夹角为30°的直线,交
夹角为30°的直线,交![]() 于点
于点![]() ,且
,且![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为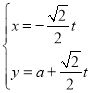 (t为参数,a∈R),以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ
(t为参数,a∈R),以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ
(1)求直线l的普通方程及曲线C的直角坐标方程;
(2)若直线l过点P(1,1)且与曲线C交于AB两点,求|PA|+|PB|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018河南豫南九校高三下学期第一次联考】设函数![]() .
.
(I)当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的范围;
的范围;
(II)若![]() 在
在![]() 处的切线为
处的切线为![]() ,且方程
,且方程![]() 恰有两解,求实数
恰有两解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为常数,
为常数, ![]() ,函数
,函数![]() ,
, ![]() (其中
(其中![]() 是自然对数的底数).
是自然对数的底数).
(1)过坐标原点![]() 作曲线
作曲线![]() 的切线,设切点为
的切线,设切点为![]() ,求证:
,求证: ![]() ;
;
(2)令![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是单调函数,求
上是单调函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
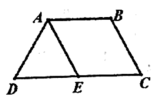
【题目】如图,等腰梯形![]() 中,
中,![]()
![]() ,
,![]() ,E为CD中点,将
,E为CD中点,将![]() 沿AE折到
沿AE折到![]() 的位置.
的位置.
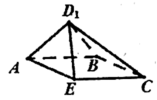
(1)证明:![]() ;
;
(2)当折叠过程中所得四棱锥![]() 体积取最大值时,求直线
体积取最大值时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com