练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知以坐标原点为圆心的圆与抛物线相交于不同的两点， ，与抛物线的准线相交于不同的两点， ，且.

    (1)求抛物线的方程；

    (2)若不经过坐标原点的直线与抛物线相交于不同的两点， ，且满足.证明直线过定点，并求出点的坐标.

    【答案】(1) 抛物线的方程为;(2) 直线过定点,证明见解析.

    【解析】试题分析：（1）由，得两点所在的直线方程为，进而根据长度求得；

    （2）设直线的方程为， 与抛物线联立得，由得，进而利用韦达定理求解即可.

    试题解析：

    （1）由已知， ，则两点所在的直线方程为

    则，故

    ∴抛物线的方程为.

    （2）由题意，直线不与轴垂直，设直线的方程为，

    .

    联立消去，得.

    ∴， ， ，

    ∵，∴

    又，

    ∴

    ∴

    解得或

    而，∴（此时）

    ∴直线的方程为，

    故直线过轴上一定点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图是一个几何体的平面展开图，其中四边形ABCD为正方形，△PDC, △PBC, △PAB, △PDA为全等的等边三角形，E、F分别为PA、PD的中点，在此几何体中，下列结论中错误的为 （ ）

    A. 平面BCD⊥平面PAD B. 直线BE与直线AF是异面直线

    C. 直线BE与直线CF共面 D. 面PAD与面PBC的交线与BC平行

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 ，且 ．
    （1）求cos2θ与 的值；
    （2）若 ，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线关于轴对称，顶点在坐标原点，直线经过抛物线的焦点.

    (1)求抛物线的标准方程；

    (2)若不经过坐标原点的直线与抛物线相交于不同的两点， ，且满足，证明直线过轴上一定点，并求出点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲袋中有1只黑球，3只红球；乙袋中有2只黑球，1只红球.

    (1)从甲袋中任取两球，求取出的两球颜色不相同的概率；

    (2)从甲，乙两袋中各取一球，求取出的两球颜色相同的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一网站营销部为统计某市网友2017年12月12日在某网店的网购情况，随机抽查了该市60名网友在该网店的网购金额情况，如下表：

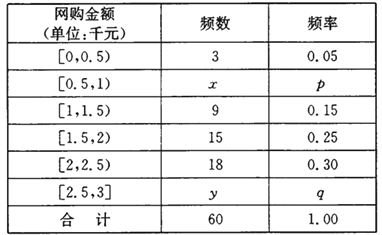
    若将当日网购金额不小于2千元的网友称为“网购达人”，网购金额小于2千元的网友称为“网购探者”.已知“网购达人”与“网购探者”人数的比例为2：3.

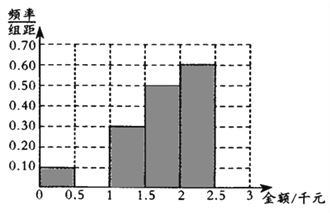
    （1）确定的值，并补全频率分布直方图；

    （2）试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数；若平均数和中位数至少有一个不低于2千元，则该网店当日被评为“皇冠店”，试判断该网店当日能否被评为“皇冠店”.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数且是定义域为R的奇函数．

    求k值；

    若，试判断函数单调性并求使不等式恒成立的t的取值范围；

    若，且在上的最小值为，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（a+2cos2x）cos（2x+θ）为奇函数，且f（ ）=0，其中a∈R，θ∈（0，π）．
    （1）求a，θ的值；
    （2）若f（ ）=﹣ ，α∈（ ，π），求sin（α+ ）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线关于轴对称，顶点在坐标原点，直线经过抛物线的焦点.

    (1)求抛物线的标准方程；

    (2)若不经过坐标原点的直线与抛物线相交于不同的两点， ，且满足，证明直线过轴上一定点，并求出点的坐标.

    查看答案和解析>>

    同步练习册答案