设数列{an}的各项都是正数,且对任意n∈N+都有an(an+1)=2(an+an…+an)
(1)求数列{an}的通项公式;
(2)设bn=a2n-2a+1,求数列{bn}的前n项和Sn;
(3)设cn=3n+(-1)n-1λ-2an(λ为非零整数,n∈N+),试确定λ的值,使得对任意n∈N+,都有cn+1>cn成立.
解:(1)由已知a
n(a
n+1)=2(a
1+…+a
n)
当n≥2时,a
n-1(a
n-1+1)=2(a
1+…+a
n-1)(1分),
两式相减,a
n(a
n+1)-a
n-1(a
n-1+1)=2a
n,a
n2-a
n-12=a
n+a
n-1因数列{a
n}的各项都是正数,∴a
n-a
n-1=1{a
n}为等差数列且公差为1,
由已知a
1=1,(4分)
∴a
n=n(5分)
(2)b
n=2n-2
n+1,(6分)
∴S
n=n(n+1)-2
n+2+4(9分)
(3)C
n=3
n+2nλ(-1)
n-1,C
n+1=3
n+1+2(n+1)λ(-1)
n,
C
n-C
n+1=3
n+1+2(n+1)λ(-1)
n-3
n-2nλ(-1)
n-1(10分)
由于C
n-C
n+1>0.
(1)当n为奇数时,C
n-C
n+1=2•3
n-2λ(2n+1)>0所以
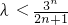
恒成立(11分)
令
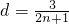
,
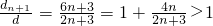
即d
n是递增数列
即为n奇数时

取最小值1,所以λ<1.(12分)
(2)当n为偶数时,所以恒成立同理知C
n-C
n+1=2•3
n+2λ(2n+1)
所以
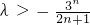
恒成立,因此当n为偶数时,
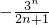
取最大值

,所以
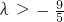
.(14分)
综上所述,λ=-1.(15分)
分析:(1)根据题中式子得到a
n-1(a
n-1+1)=2(a
1+…+a
n-1)两者相减即可得到数列{a
n}的通项公式;
(2)根据(10所求的a
n,可得b
n,进而求出数列{b
n}的前n项和S
n,
(3)求出C
n-C
n+1的值,对n是奇数偶数分别讨论,从而确定λ的值.
点评:此题主要考查数列通项公式和前前n项和的求解.

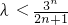 恒成立(11分)
恒成立(11分)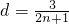 ,
,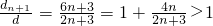 即dn是递增数列
即dn是递增数列 取最小值1,所以λ<1.(12分)
取最小值1,所以λ<1.(12分)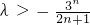 恒成立,因此当n为偶数时,
恒成立,因此当n为偶数时,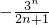 取最大值
取最大值 ,所以
,所以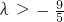 .(14分)
.(14分)
