练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，△ABC的角平分线AD的延长线交它的外接圆于点E.

    (1)证明：△ABE∽△ADC；

    (2)若△ABC的面积S＝AD·AE，求∠BAC的大小．

     

    （1）见解析（2）90°

    【解析】(1)由已知条件，可得∠BAE＝∠CAD.因为∠AEB与∠ACB是同弧上的圆周角，所以∠AEB＝∠ACD.故△ABE∽△ADC.

    (2)因为△ABE∽△ADC，所以，

    即AB·AC＝AD·AE.

    又S＝AB·ACsin∠BAC，且S＝AD·AE，

    故AB·AC·sin∠BAC＝AD·AE.

    则sin∠BAC＝1，又∠BAC为三角形内角，所以∠BAC＝90°

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练优化重组卷5练习卷（解析版） 题型：选择题

    已知抛物线y2＝8x的准线与双曲线－y2＝1(m>0)交于A，B两点，点F为抛物线的焦点，若△FAB为直角三角形，则双曲线的离心率是(　　)．

    A. B. C．2 D．2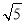

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练优化重组卷2练习卷（解析版） 题型：解答题

    已知函数f(x)＝Msin(ωx＋φ)(M>0，ω>0，|φ|<)的部分图象如图所示．

    (1)求函数f(x)的解析式；

    (2)在△ABC中，角A，B，C的对边分别是a，b，c，若(2a－c)cos B＝bcos C，求f的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练优化重组卷1练习卷（解析版） 题型：填空题

    一出租车司机从饭店到火车站的途中经过六个交通岗，假设他在各交通岗遇到红灯这一事件是相互独立的，并且概率都是.那么这位司机遇到红灯前，已经通过了两个交通岗的概率是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练x4-1练习卷（解析版） 题型：解答题

    如图，直线AB为圆O的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于点D.

    (1)证明：DB＝DC；

    (2)设圆的半径为1，BC＝，延长CE交AB于点F，求△BCF外接圆的半径．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练x4-1练习卷（解析版） 题型：填空题

    如图，已知Rt△ABC的两条直角边AC，BC的长分别为3 cm，4 cm，以AC为直径的圆与AB交于点D，则BD＝________cm.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练x4-1练习卷（解析版） 题型：填空题

    如图，已知PA，PB是圆O的切线，A，B分别为切点，C为圆O上不与A，B重合的另一点，若∠ACB＝120°，则∠APB＝________.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练5练习卷（解析版） 题型：解答题

    设函数f(x)＝ax－(1＋a2)x2，其中a>0，区间I＝{x|f(x)>0}．

    (1)求I的长度(注：区间(α，β)的长度定义为β－α)；

    (2)给定常数k∈(0,1)，当1－k≤a≤1＋k时，求I长度的最小值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练2练习卷（解析版） 题型：选择题

    “a>3”是“函数f(x)＝ax＋3在(－1,2)上存在零点”的 (　　)．

    A．充分不必要条件 B．必要不充分条件

    C．充要条件 D．既不充分也不必要条件

     

    查看答案和解析>>

    同步练习册答案