
| A. | p∧q | B. | ?p∧?q | C. | ?p∧q | D. | p∧?q |
分析 复合命题的真假判定,解决的办法是先判断组成复合命题的简单命题的真假,再进一步进行判断,则答案可求.
解答 解:函数y=2-ax+1的图象可看作把y=ax的图象先沿轴反折,再左移1各单位,最后向上平移2各单位得到,而y=ax的图象恒过(0,1),
∴函数y=2-ax+1恒过(-1,1)点,
∴命题p假,则¬p真.
函数f(x-1)为偶函数,则其对称轴为x=0,而函数f(x)的图象是把y=f(x-1)向左平移了1各单位,
∴f(x)的图象关于直线x=-1对称,
∴命题q假,则命题¬q真.
综上可知,命题¬p∧¬q为真命题.
故选:B.
点评 本题考查了复合命题的真假判定,考查了函数的性质,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | (2,+∞) | C. | [$\sqrt{2}$,+∞) | D. | ($\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
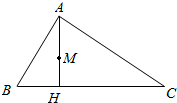 如图,在△ABC中,AB=2,BC=3,∠ABC=60°,AH⊥BC于点H,M为AH的中点,若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$,则λ+μ=$\frac{2}{3}$.
如图,在△ABC中,AB=2,BC=3,∠ABC=60°,AH⊥BC于点H,M为AH的中点,若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$,则λ+μ=$\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
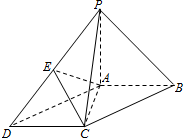 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015+2016i | B. | 2015-2016i | C. | -2016+2015i | D. | -2016-2015i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
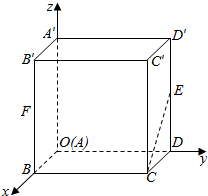 如图,空间直角坐标系中由长方体ABCD-A′B′C′D′,AB=1,BC=2,AA′=2,E和F分别是棱DD′和BB′的中点.证明:CE∥A′F,并求它们之间的距离.
如图,空间直角坐标系中由长方体ABCD-A′B′C′D′,AB=1,BC=2,AA′=2,E和F分别是棱DD′和BB′的中点.证明:CE∥A′F,并求它们之间的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com