练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3名志愿者在10月1日至10月5日期间参加社区服务工作，若每名志愿者在这5天中任选两天参加社区服务工作，且各名志愿者的选择互不影响．求
    （Ⅰ）这3名志愿者中在10月1日都参加社区服务工作的概率；
    （Ⅱ）这3名志愿者中在10月1日至多有1人参加社区服务工作的概率．
    解法一：（I）这3名志愿者中在10月1号参加社区服务工作的人数恰好为3人的事件为A
    P(A)=
    (
    C14
    )    3
    (
    C25
    )    3
    =
    8
    125

    这3名志愿者中在10月1号参加社区服务工作的人数恰好为3人的概率为
    8
    125
    ．
    （Ⅱ）这3名志愿者中在10月1号参加社区服务工作的人数至多为1人的事件为B
    P(B)=
    (
    C24
    )    3
    (
    C25
    )    3
    +
    C13
    C14
    (
    C24
    )    2
    (
    C25
    )    3
    =
    27
    125
    +
    54
    125
    =
    81
    125

    这3名志愿者中在10月1号参加社区服务工作的人数至多为1人的概率为
    81
    125
    ．
    解法二：
    （I）这3名志愿者中在10月1号参加社区服务工作的人数恰好为3人的事件为A
    P(A)=(
    2
    5
    )3=
    8
    125

    这3名志愿者中在10月1号参加社区服务工作的人数恰好为3人的概率为
    8
    125
    ．
    （Ⅱ）这3名志愿者中在10月1号参加社区服务工作的人数至多为1人的事件为B
    P(B)=(
    3
    5
    )3+
    C13
    (
    2
    5
    )(
    3
    5
    )2=
    27
    125
    +
    54
    125
    =
    81
    125

    这3名志愿者中在10月1号参加社区服务工作的人数至多为1人的概率为
    81
    125
    ．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    3名志愿者在10月1号至10月5号期间参加社区服务工作．
    （Ⅰ）若每名志愿者在这5天中任选一天参加社区服务工作，且各志愿者的选择互不影响，求3名志愿者恰好连续3天参加社区服务工作的概率；
    （Ⅱ）若每名志愿者在这5天中任选两天参加社区服务工作，且各志愿者的选择互不影响，记ξ表示这3名志愿者在10月1号参加社区服务工作的人数，求随机变量ξ的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    3名志愿者在10月1日至10月5日期间参加社区服务工作，若每名志愿者在这5天中任选两天参加社区服务工作，且各名志愿者的选择互不影响．求
    （Ⅰ）这3名志愿者中在10月1日都参加社区服务工作的概率；
    （Ⅱ）这3名志愿者中在10月1日至多有1人参加社区服务工作的概率．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年辽宁省丹东市宽甸二中高二下学期期末考试数学（理） 题型：解答题

    (本小题满分12分)
    已知3名志愿者在10月1号至10月5号期间参加2011年国庆节志愿者活动工作．
    （1）若每名志愿者在5天中任选一天参加社区服务工作，且各志愿者的选择互不影响，求3名志原者恰好连续3天参加社区服务工作的概率；
    （2）若每名志愿者在这5天中任选两天参加社区服务工作，且各志愿者的选择互不影响，记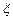表示这3名志愿者在10月1号参加志愿者服务工作的人数，求随机变量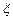的数学期望．

    查看答案和解析>>

    科目：高中数学 来源：2012届辽宁省丹东市高二下学期期末考试数学（理） 题型：解答题

    (本小题满分12分)

    已知3名志愿者在10月1号至10月5号期间参加2011年国庆节志愿者活动工作．

    （1）若每名志愿者在5天中任选一天参加社区服务工作，且各志愿者的选择互不影响，求3名志原者恰好连续3天参加社区服务工作的概率；

    （2）若每名志愿者在这5天中任选两天参加社区服务工作，且各志愿者的选择互不影响，记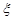表示这3名志愿者在10月1号参加志愿者服务工作的人数，求随机变量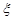的数学期望．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3名志愿者在10月1日至10月5日期间参加社区服务工作，若每名志愿者在这5天中任选两天参加社区服务工作，且各名志愿者的选择互不影响．求
    （Ⅰ）这3名志愿者中在10月1日都参加社区服务工作的概率；
    （Ⅱ）这3名志愿者中在10月1日至多有1人参加社区服务工作的概率．

    查看答案和解析>>

    同步练习册答案