
【题目】高二年级举行一次演讲赛共有10位同学参赛,其中一班有3位,二班有2位,其它班有5位,若采用抽签的方式确定他们的演讲顺序,则一班有3位同学恰好被排在一起(指演讲序号相连),而二班的2位同学没有被排在一起的概率为:( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】解:由题意知本题是一个古典概型,
∵试验发生包含的所有事件是10位同学参赛演讲的顺序共有: ![]() ;
;
满足条件的事件要得到“一班有3位同学恰好被排在一起而二班的2位同学没有被排在一起的演讲的顺序”可通过如下步骤:
①将一班的3位同学“捆绑”在一起,有![]() 种方法;
种方法;
②将一班的“一梱”看作一个对象与其它班的5位同学共6个对象排成一列,有![]() 种方法;
种方法;
③在以上6个对象所排成一列的7个间隙(包括两端的位置)中选2个位置,将二班的2位同学插入,有![]() 种方法.
种方法.
根据分步计数原理(乘法原理),共有![]()
![]()
![]() 种方法.
种方法.
∴一班有3位同学恰好被排在一起(指演讲序号相连),
而二班的2位同学没有被排在一起的概率为:P=![]()
![]()
![]()
![]() =
=![]()
故选B.


科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)若![]() ,求直线
,求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 有两个不同的交点,求
有两个不同的交点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.

(1) 经计算估计这组数据的中位数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取
的芒果中随机抽取![]() 个,再从这
个,再从这![]() 个中随机抽取
个中随机抽取![]() 个,求这
个,求这![]() 个芒果中恰有
个芒果中恰有![]() 个在
个在![]() 内的概率.
内的概率.
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有![]() 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:
A:所以芒果以![]() 元/千克收购;
元/千克收购;
B:对质量低于![]() 克的芒果以
克的芒果以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.
元/个收购.
通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为F1,F2,离心率为
的左右焦点分别为F1,F2,离心率为![]() ,设过点F2的直线l被椭圆C截得的线段为MN,当l⊥x轴时,|MN|=3.
,设过点F2的直线l被椭圆C截得的线段为MN,当l⊥x轴时,|MN|=3.
(1)求椭圆C的标准方程;
(2)在x轴上是否存在一点P,使得当l变化时,总有PM与PN所在的直线关于x轴对称?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系中,直线
轴的正半轴为极轴建立极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求C的普通方程和直线![]() 的倾斜角;
的倾斜角;
(Ⅱ)设点![]() (0,2),
(0,2),![]() 和
和![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乡镇政府为了解决农村教师的住房问题,计划征用一块土地盖一幢建筑总面积为10000![]() 公寓楼(每层的建筑面积相同).已知士地的征用费为
公寓楼(每层的建筑面积相同).已知士地的征用费为![]() ,土地的征用面积为第一层的
,土地的征用面积为第一层的![]() 倍,经工程技术人员核算,第一层建筑费用为
倍,经工程技术人员核算,第一层建筑费用为![]() ,以后每增高一层,其建筑费用就增加
,以后每增高一层,其建筑费用就增加![]() ,设这幢公寓楼高层数为n,总费用为
,设这幢公寓楼高层数为n,总费用为![]() 万元.(总费用为建筑费用和征地费用之和)
万元.(总费用为建筑费用和征地费用之和)
(1)若总费用不超过835万元,求这幢公寓楼最高有多少层数?
(2)试设计这幢公寓的楼层数,使总费用最少,并求出最少费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形![]() 是矩形,
是矩形,![]() ,将
,将![]() 沿着对角线AC翻折,得到
沿着对角线AC翻折,得到![]() ,设顶点
,设顶点![]() 在平面
在平面![]() 上的投影为O.
上的投影为O.
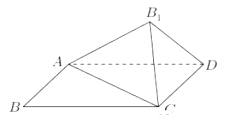
(1)若点O恰好落在边AD上,①求证:![]() 平面
平面![]() ;②若
;②若![]() ,
,![]() ,当BC取到最小值时,求k的值;
,当BC取到最小值时,求k的值;
(2)当![]() 时,若点O恰好落在
时,若点O恰好落在![]() 的内部(不包括边界),求二面角
的内部(不包括边界),求二面角![]() 的余弦值的取值范围.
的余弦值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() 在区间
在区间![]() 上不是单调函数,求实数
上不是单调函数,求实数![]() 的范围;
的范围;
(2)若对任意![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,设
时,设![]() ,对任意给定的正实数
,对任意给定的正实数![]() ,曲线
,曲线![]() 上是否存在两点
上是否存在两点![]() ,
,![]() ,使得
,使得![]() 是以
是以![]() (
(![]() 为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在![]() 轴上?请说明理由.
轴上?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com