
| A. | (0,100) | B. | (1,100) | C. | (0,10) | D. | (10,100) |
分析 令g(a)=a(lgx-1)+1,由题意可得$\left\{\begin{array}{l}{g(-1)>0}\\{g(1)>0}\end{array}\right.$,由对数不等式的解法,即可得到所求范围.
解答 解:令g(a)=a(lgx-1)+1,
由题意可得$\left\{\begin{array}{l}{g(-1)>0}\\{g(1)>0}\end{array}\right.$,
即为$\left\{\begin{array}{l}{-(lgx-1)+1>0}\\{lgx-1+1>0}\end{array}\right.$,
即有$\left\{\begin{array}{l}{0<x<100}\\{x>10}\end{array}\right.$,
解得10<x<100.
故选:D.
点评 本题考查函数的单调性的运用:解不等式,注意构造一次函数,运用一次函数的单调性,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | a | b | c | a+b+c |
| f(x) | d | d | t | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
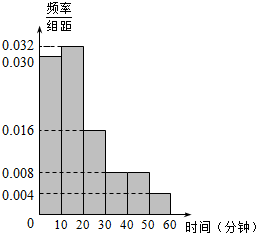 某校决定为本校上学时间不少于30分钟的学生提供校车接送服务.为了解学生上学所需时间,从全校600名学生中抽取50人统计上学时间(单位:分钟),现对600人随机编号为001,002,…600.抽取50位学生上学时间均不超过60分钟,将时间按如下方式分成六组,第一组上学时间在[0,10),第二组上学时间在[10,20),…第六组上学时间在[50,60]得到各组人数的频率分布直方图.如图.
某校决定为本校上学时间不少于30分钟的学生提供校车接送服务.为了解学生上学所需时间,从全校600名学生中抽取50人统计上学时间(单位:分钟),现对600人随机编号为001,002,…600.抽取50位学生上学时间均不超过60分钟,将时间按如下方式分成六组,第一组上学时间在[0,10),第二组上学时间在[10,20),…第六组上学时间在[50,60]得到各组人数的频率分布直方图.如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com