Question

4．定义在R上的偶函数f（x）满足f（x）-f（x+2）=0，且当x∈[0，2]时，f（x）=2sin$\frac{π}{2}$x，记sgn（x）=$\left\{\begin{array}{l}{x，x＞0}\\{0，x=0}\\{-x，x＜0}\end{array}\right.$，则函数y=f（x）-sgn（log₂（sgn（x）））的零点个数为（　　）

• A． 3
• B． 4
• C． 6
• D． 8

Answer 1

分析 先将函数sgn（x）转化为函数g（x）=|x|，再分别画出两函数的图象，并根据函数图象确定方程解的个数．

解答 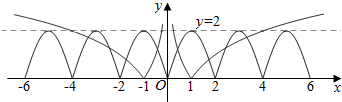解：根据题中函数sgn（x）的解析式知，
sgn（x）=|x|，所以，
记g（x）=sgn（log₂（sgn（x）））=|log₂|x||，
画出g（x）的图象，如右图红线，
再考察函数f（x），分析如下：
因为，f（x+2）=f（x），所以，f（x）是以2为周期的函数，
且当x∈[0，2]，f（x）=2sin$\frac{π}{2}$x，画出f（x）的图象如右图紫线，
当x=±5时，f（x）=2，
所以，当x＞5或x＜-5时，f（x）＞2，两图象无公共点，
由图可知，两图象有8个交点，所以原函数有8个零点，
故答案为：D．

点评 本题主要考查了根的存在和个数的判断，涉及对数函数、三角函数的图象与性质，体现了数形结合的解题思想，属于中档题．