
分析 根据x2+3>0化简不等式,结合条件、一元二次不等式的解法,根与系数的关系列出不等式组,即可求出k的值.
解答 解:∵x2+3>0,∴$\frac{4x}{{x}^{2}+3}≤k$化为kx2-4x+3k≥0,
∵不等式$\frac{4x}{{x}^{2}+3}$≤k的解集为[-3,-1],
∴不等式kx2-4x+3k≥0 的解集为[-3,-1],
则-3、-1是方程的kx2-4x+3k=0 两个根,
即$\left\{\begin{array}{l}{k<0}\\{\frac{4}{k}=-3-1}\end{array}\right.$,解得k=-1,
∴k的值是-1.
点评 本题考查分式不等式的转化,一元二次不等式的解法,以及根与系数的关系,考查化简、变形能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
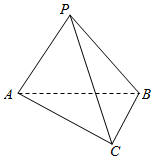 如图,把等腰直角三角形ABC以斜边AB为轴旋转,使C点移动的距离等于AC时停止,并记为点P.
如图,把等腰直角三角形ABC以斜边AB为轴旋转,使C点移动的距离等于AC时停止,并记为点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
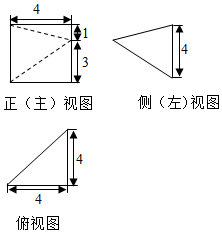 一锥体的三视图如图所示,设该棱锥的最长棱和最短棱的棱长分别为m,n,则$\frac{m}{n}$等于( )
一锥体的三视图如图所示,设该棱锥的最长棱和最短棱的棱长分别为m,n,则$\frac{m}{n}$等于( )| A. | $\frac{\sqrt{33}}{4}$ | B. | $\frac{\sqrt{41}}{3}$ | C. | $\frac{\sqrt{41}}{4}$ | D. | $\frac{\sqrt{33}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 135° | C. | 45°或135° | D. | 75°或105° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-3i | B. | 1+3i | C. | -1+3i | D. | -1-3i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com