考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)首先根据长方体的性质,得到线面垂直,进一步转化成线线垂直,同理得到另一对线线垂直,最后得到线面垂直.
(Ⅱ)首先建立空间直角坐标系利用线面垂直得到平面的法向量,利用上步的结论进一步得到平面AEF的法向量,最后利用法向量的夹角求出二面角的余弦值.
解答:
(Ⅰ)证明:在长方体A BCD-A
1B
1C
1D
1中,
BC⊥平面AA
1B
1B,AE?平面AA
1B
1B
所以:BC⊥AE,
由于AE⊥A
1B
所以:AE⊥平面A
1BC
AE⊥A
1C①
同理:DC⊥平面ADD
1A
1,AF?平面ADD
1A
1,
所以:DC⊥AF
由于:AF⊥A
1D
所以:AF⊥平面A
1CD
AF⊥A
1C②
由①②知:A
1C⊥平面AEF
(Ⅱ)解:分别以AB,AD,AA
1为x轴,y轴,z轴,建立空间直角坐标系,连接AC,
由于:AB=4,AD=3,AA
1=5
所以:
=(4,3,0),
=(-4,3,0),
=(0,0,5)由于:
•=0,
•=0所以:AC⊥DD
1,AC⊥BD
AC⊥平面DBB
1D
1所以可以把
看做是平面DBB
1D
1的法向量.
又由于:AC
1⊥平面AEF
所以:
看做是平面AEF的法向量.
=(4,3,-5)设平面AEF和平面D
1B
1BD所成的角为θ
则:cosθ=|
|=
所以:平面AEF和平面D
1B
1BD所成的角的余弦值为
.
点评:本题考查的知识要点:面面垂直与线面垂直间的转化及线面垂直的判定定理,空间直角坐标系,法向量,二面角的应用,属于中等题型.

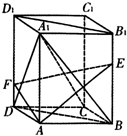 如图,在长方体A BCD-A1B1C1D1中,点E,F分别在BB1,DD1上,且AE⊥A1B,AF⊥A1D.
如图,在长方体A BCD-A1B1C1D1中,点E,F分别在BB1,DD1上,且AE⊥A1B,AF⊥A1D.

 如图,O为坐标原点,点A,B在⊙O上,且点A在第一象限,点B(-
如图,O为坐标原点,点A,B在⊙O上,且点A在第一象限,点B(-