
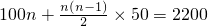


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2010•烟台一模)某地区有荒山2200亩,从2009年开始每年年初在荒山上植树造林,第一年植树100亩,以后每年比上一年多植树50亩.如图,某同学设计了一个程序框图计算到哪一年可以将荒山全部绿化(假定所植树全部成活),则框图
(2010•烟台一模)某地区有荒山2200亩,从2009年开始每年年初在荒山上植树造林,第一年植树100亩,以后每年比上一年多植树50亩.如图,某同学设计了一个程序框图计算到哪一年可以将荒山全部绿化(假定所植树全部成活),则框图 应填上的条件是
应填上的条件是查看答案和解析>>
科目:高中数学 来源: 题型:
 某地区有荒山2200亩,从2002年开始每年年初在荒山上植树造林,第一年植树100亩,以后每年比上一年多植树50亩.
某地区有荒山2200亩,从2002年开始每年年初在荒山上植树造林,第一年植树100亩,以后每年比上一年多植树50亩.查看答案和解析>>
科目:高中数学 来源:广州三模 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:
某地区有荒山2200亩,从2002年开始每年年初在荒山上植树造林,
第一年植树100亩,以后每年比上一年多植树50亩.
(1)若所植树全部成活,则到哪一年可以将荒山全部绿化?
(2)若每亩所植树苗木材量为2立方米,每年树木木材量的自然增长率
为20%,那么到全部绿化后的那一年年底,该山木材总量是多少?
(精确到1立方米, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com