
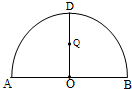
 如图所示,为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
如图所示,为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.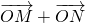 与
与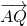 平行,若平行,求出直线l的方程,若不平行,请说明理由.
平行,若平行,求出直线l的方程,若不平行,请说明理由.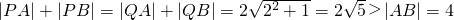

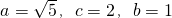 所以所求椭圆C的方程为
所以所求椭圆C的方程为 (5分)
(5分)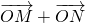 与
与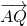 平行,设直线l方程为y=kx+2
平行,设直线l方程为y=kx+2 消去Y,整理得(5k2+1)x2+20kx+15=0,(7分)
消去Y,整理得(5k2+1)x2+20kx+15=0,(7分) .
. ,
,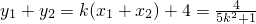 (9分)
(9分) ,
,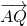 =(2,1)
=(2,1)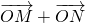 与
与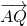 平行
平行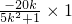 =
= ∴
∴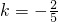 (11分)
(11分)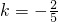 与
与 矛盾
矛盾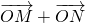 与
与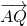 平行(12分)
平行(12分)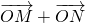 与
与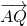 平行,求出对应的斜率看是否符合要求即可.
平行,求出对应的斜率看是否符合要求即可.

 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:

| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•武昌区模拟)已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:
(2012•武昌区模拟)已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com