已知f(n)＝1＋
n∈N?)，g(n)＝2(
－1)(n∈N?)．
(1)当n＝1，2，3时，分别比较f(n)与g(n)的大小(直接给出结论)；
(2)由(1)猜想f(n)与g(n)的大小关系，并证明你的结论．
名校课堂系列答案科目：高中数学 来源： 题型：解答题
观察下表：
1，
2,3
4,5,6,7
8,9,10,11,12,13,14,15，
…
问：(1)此表第n行的最后一个数是多少？
(2)此表第n行的各个数之和是多少？
(3)2 008是第几行的第几个数？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
若实数x、y、m满足|x－m|＞|y－m|，则称x比y远离m.
(1)若x2－1比1远离0，求x的取值范围；
(2)对任意两个不相等的正数a、b，证明：a3＋b3比a2b＋ab2远离2ab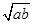
.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：
①sin213°＋cos217°－sin 13°cos 17°；
②sin215°＋cos215°－sin 15°cos 15°；
③sin218°＋cos212°－sin 18°cos 12°；
④sin2(－18°)＋cos248°－sin(－18°)cos 48°；
⑤sin2(－25°)＋cos255°－sin(－25°)cos 55°.
(1)试从上述五个式子中选择一个，求出这个常数；
(2)根据(1)的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知下列三个方程：x2＋4ax－4a＋3＝0，x2＋(a－1)x＋a2＝0，x2＋2ax－2a＝0，其中至少有一个方程有实根，求实数a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
，
，求证：
，
，
．
是菱形，
是矩形，
平面
，
．
平面
；
为直二面角，求直线
与平面
所成的角
的正弦值．