
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 、
、![]() 为椭圆
为椭圆![]() 的两焦点,
的两焦点,![]() 的周长为
的周长为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设椭圆![]() ,曲线
,曲线![]() 的切线
的切线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,试证:
两点,试证:![]() 的面积为定值.
的面积为定值.
【答案】见解析
【解析】(Ⅰ)由题意得:![]() ,
,![]() ,………………2分
,………………2分
则![]() ,
,![]() ,所以
,所以![]() , ………………3分
, ………………3分
故椭圆C的标准方程为![]() . ………………4分
. ………………4分
(Ⅱ)设![]() ,
,![]() ,
,
将![]() 代入椭圆
代入椭圆![]() 的方程,消去
的方程,消去![]() 可得
可得![]() ,
,
显然直线与椭圆![]() 的切点在椭圆
的切点在椭圆![]() 内,所以
内,所以![]() ,
,
由根与系数的关系得![]() ,
,![]() , …………………6分
, …………………6分
所以![]() , …………………………………………………7分
, …………………………………………………7分
因为直线![]() 与
与![]() 轴交点的坐标为
轴交点的坐标为![]() ,
,
所以![]() 的面积
的面积![]() …………………9分
…………………9分
![]() ,…………11分
,…………11分
设![]() ,
,
将![]() 代入椭圆
代入椭圆![]() 的方程,可得
的方程,可得![]() , ………12分
, ………12分
由![]() ,可得
,可得![]() ,即
,即![]() , …………………………………………13分
, …………………………………………13分
又![]() ,故
,故![]() 的面积为定值. ………………………14分
的面积为定值. ………………………14分
【命题意图】本题主要考查直线的方程、椭圆的方程与性质、直线与圆、直线与椭圆的位置关系以及圆锥曲线中的定值与范围问题,考查最基本的运算能力以及逻辑推理能力、方程的思想等,是难题.


科目:高中数学 来源: 题型:
【题目】设函数g(x)=3x , h(x)=9x .
(1)解方程:h(x)﹣8g(x)﹣h(1)=0;
(2)令p(x)= ![]() ,求值:p(
,求值:p( ![]() )+p(
)+p( ![]() )+…+p(
)+…+p( ![]() )+p(
)+p( ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某消防机构为![]() 四个小区的居民代表进行消防安全知识宣传.在代表中,按分层抽样的方式抽取了10名“幸运之星”,“幸运之星”每人获得一份纪念品.相关数据如下:
四个小区的居民代表进行消防安全知识宣传.在代表中,按分层抽样的方式抽取了10名“幸运之星”,“幸运之星”每人获得一份纪念品.相关数据如下:
小区 | A | B | C | D |
代表人数 | 45 | 60 | 30 | 15 |
(I)求此活动中各小区“幸运之星”的人数;
(II)从B小区和C小区的“幸运之星”中任选两人进行后续的活动,求这两个人均来自B小区的概率;
(III)消防机构在B小区内,对参加问答活动的居民进行了是否有兴趣参加消防安全培训的问卷调查,统计结果如下(单位:人):
有兴趣 | 无兴趣 | 合计 | |
男 | 25 | 5 | 30 |
女 | 15 | 15 | 30 |
合计 | 40 | 20 | 60 |
据此判断能否在犯错误的概率不超过![]() 的前提下认为有兴趣参加消防安全培训与性别有关系?
的前提下认为有兴趣参加消防安全培训与性别有关系?
临界值表:
|
|
|
|
|
|
|
|
|
|
参考公式: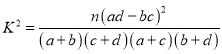 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二手车经销商小王对其所经营的![]() 型号二手汽车的使用年数
型号二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下数据:
(单位:万元/辆)进行整理,得到如下数据:
使用年数 | 2 | 3 | 4 | 5 | 6 | 7 |
售价 | 20 | 12 | 8 | 6.4 | 4.4 | 3 |
| 3.00 | 2.48 | 2.08 | 1.86 | 1.48 | 1.10 |
下面是![]() 关于
关于![]() 的散点图:
的散点图:
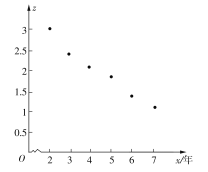
(I)由散点图看出,可以用线性回归模型拟合![]() 和
和![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(II)求![]() 关于
关于![]() 的回归方程,并预测某辆
的回归方程,并预测某辆![]() 型号二手汽车当使用年数为9年时,售价大约为多少?(
型号二手汽车当使用年数为9年时,售价大约为多少?(![]() 、
、![]() 的值精确到
的值精确到![]() )
)
(III)基于成本的考虑,该型号二手汽车的售价不得低于7118元,请根据(II)求出的回归方程预测在收购该型号二手汽车时,车辆的使用年数不得超过多少年?
参考公式: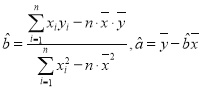 ,相关系数
,相关系数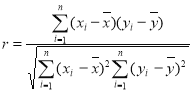 .
.
参考数据:![]() ,
,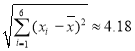 ,
,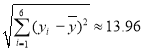 ,
,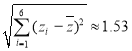 ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新生儿Apgar评分,即阿氏评分是对新生儿出生后总体状况的一个评估,主要从呼吸、心率、反射、肤色、肌张力这几个方面评分,满10分者为正常新生儿,评分7分以下的新生儿考虑患有轻度窒息,评分在4分以下考虑患有重度窒息,大部分新生儿的评分多在7-10分之间,某市级医院妇产科对1月份出生的新生儿随机抽取了16名,以下表格记录了他们的评分情况.
(1)现从16名新生儿中随机抽取3名,求至多有1名评分不低于9分的概率;
(2)以这16名新生儿数据来估计本年度的总体数据,若从本市本年度新生儿任选3名,记![]() 表示抽到评分不低于9分的新生儿数,求
表示抽到评分不低于9分的新生儿数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点 ,离心率为
,离心率为![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 的长轴的两个端点(
的长轴的两个端点(![]() 位于
位于![]() 右侧),
右侧),![]() 是椭圆在
是椭圆在![]() 轴正半轴上的顶点.
轴正半轴上的顶点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 和
和![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求出直线方程;如果不存在,请说明理由.
共线?如果存在,求出直线方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A、B、C的对边分别为a、b、c,a=btanA,且B为钝角.
(1)证明:B﹣A= ![]() ;
;
(2)求sinA+sinC的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人想参加《中国诗词大会》比赛,筹办方要从10首诗司中分别抽出3首让甲、乙背诵,规定至少背出其中2首才算合格; 在这10首诗词中,甲只能背出其中的7首,乙只能背出其中的8首
(1)求抽到甲能背诵的诗词的数量![]() 的分布列及数学期望;
的分布列及数学期望;
(2)求甲、乙两人中至少且有一人能合格的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com