
【题目】已知数列{an}的前n项和为Sn , a1=1,an≠0,anan+1=4Sn﹣1.
(Ⅰ)求{an}的通项公式;
(Ⅱ)证明: ![]() +
+ ![]() +…+
+…+ ![]() <2.
<2.
【答案】(I)解:由题设,anan+1=4Sn﹣1,得an+1an+2=4Sn+1﹣1.
两式相减得an+1(an+2﹣a)=4an+1.
由于an+1≠0,∴an+2﹣an=4.
由题设,a1=1,a1a2=4S1﹣1,可得a2=3.
故可得{a2n﹣1}是首项为1,公差为4的等差数列,a2n﹣1=4n﹣3=2(2n﹣1)﹣1;
{a2n}是首项为3,公差为4的等差数列,a2n=4n﹣1=22n﹣1.
∴ ![]() ;
;
(Ⅱ)证明: ![]() ,
,
当n>1时,由 ![]() ,得
,得
![]() ,
,
∴ ![]()
【解析】(Ⅰ)化简anan+1=4Sn﹣1求得数列{an}的特点,进而求得数列{an}的通项公式;(Ⅱ)根据(Ⅰ)求得数列的前n项和,代入后求得所给不等式成立.
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系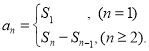 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】设正三棱锥A﹣BCD(底面是正三角形,顶点在底面的射影为底面中心)的所有顶点都在球O的球面上,BC=2,E,F分别是AB,BC的中点,EF⊥DE,则球O的表面积为( )
A.![]()
B.6π
C.8π
D.12π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四棱锥P﹣ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2 ![]() ,BC=4
,BC=4 ![]() ,PA=2,点M在线段PD上.
,PA=2,点M在线段PD上.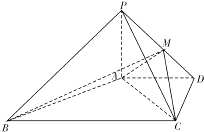
(1)求证:AB⊥PC.
(2)若二面角M﹣AC﹣D的大小为45°,求BM与平面PAC所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】脱贫是政府关注民生的重要任务,了解居民的实际收入状况就显得尤为重要.现从某地区随机抽取![]() 个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第
个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第![]() 个农户的年收入
个农户的年收入![]() (万元),年积蓄
(万元),年积蓄![]() (万元),经过数据处理得
(万元),经过数据处理得![]()
(Ⅰ)已知家庭的年结余![]() 对年收入
对年收入![]() 具有线性相关关系,求线性回归方程;
具有线性相关关系,求线性回归方程;
(Ⅱ)若该地区的农户年积蓄在![]() 万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?
万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?
附:在![]() 中,
中, 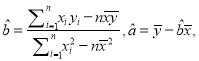 其中
其中![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+2ax﹣a﹣1,x∈[0,2],a为常数.
(1)用g(x)表示f(x)的最小值,求g(a)的解析式;
(2)在(1)中,是否存在最小的整数m,使得g(a)﹣m≤0对于任意a∈R均成立,若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)如果对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,使得函数
,使得函数![]() 的最大值为0,若存在,求出
的最大值为0,若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com