分析:把已知等式左边的第二项利用二倍角的余弦函数公式化简,移项合并后,由B=π-(A+C)再利用诱导公式变形,和差化积后得到sinAsinC的值,然后根据三边a,b,c成等比数列,由等差数列的性质列出关系式,利用正弦定理化简后,把求出的sinAsinC的值代入,开方可得出sinB的值,根据B为三角形的内角,利用特殊角的三角函数值求出B的度数.
解答:解:由已知得:cos(A-C)+cosB=
,
cos(A-C)+cos(A+C)=
,
∴sinAsinC=
,
又∵a,b,c成等比数列,∴b
2=ac,
又由正弦定理得sin
2B=sinA•sinC,
∴sin
2B=
,sinB=,(-舍去),
∴B=60°或120°,
但若B=120°,则有b>a,b>c,b
2>ac,
这与已知b
2=ac矛盾,故B≠120°,
∴B=60°
点评:此题考查了二倍角的余弦函数公式,诱导公式,等差数列的性质,以及正弦定理,利用了整体代入的思想.学生在求值时注意根据角度的范围做到合理的取舍,例如求sinB值时,舍去负值是因为B为三角形的内角,不可能取负值;求出B度数后,利用了反证法说明了B≠120°,进而得出了满足题意的B的度数.



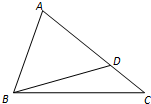 如图,在△ABC中,cos∠ABC=
如图,在△ABC中,cos∠ABC=