
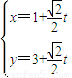 ��t������
��tΪ������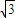 ���õ�����C3��PΪ����C3��һ���㣬���P��ֱ��C2�ľ������Сֵ���������Ӧ��P������꣮
���õ�����C3��PΪ����C3��һ���㣬���P��ֱ��C2�ľ������Сֵ���������Ӧ��P������꣮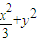 =1�����P��
=1�����P��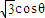 ��sin�ȣ�����P��ֱ�ߵľ���Ϊd=
��sin�ȣ�����P��ֱ�ߵľ���Ϊd=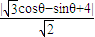 =
=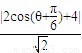 ���������Ǻ�����������⣮
���������Ǻ�����������⣮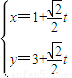 ��tΪ��������
��t��������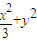 =1
=1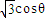 ��sin�ȣ�����P��ֱ�ߵľ���Ϊd=
��sin�ȣ�����P��ֱ�ߵľ���Ϊd=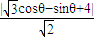 =
=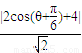
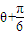 =���ǣ�dȡ����Сֵ
=���ǣ�dȡ����Сֵ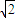 ����ʱ
����ʱ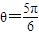 ��
��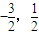 ��
��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
| �� |
| 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| 12 |
| y2 |
| 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ���⣨1����2����3������ѡ���⣬ÿС��5�֣��뿼����ѡ1�����������������������ǰ1��Ʒ֣�
���⣨1����2����3������ѡ���⣬ÿС��5�֣��뿼����ѡ1�����������������������ǰ1��Ʒ֣�| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| 2 |
| 3�� |
| 4 |
| 2 |
| 3�� |
| 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| �� |
| 3 |
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
| �� |
| 4 |
| ||
| 2 |
| ||
| 3 |
| ||
| 3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com