
【题目】![]() 请用空间向量求解
请用空间向量求解![]() 已知正四棱柱
已知正四棱柱![]() 中,
中,![]() ,
,![]() ,
, ![]() 分别是棱
分别是棱![]() ,
,![]() 上的点,且满足
上的点,且满足![]() ,
,![]() .
.
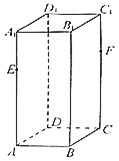
![]() 求异面直线
求异面直线![]() ,
,![]() 所成角的余弦值;
所成角的余弦值;
![]() 求面
求面![]() 与面
与面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
![]() 推导出AD,DC,
推导出AD,DC,![]() 两两垂直,以A为原点,DA,DC,
两两垂直,以A为原点,DA,DC,![]() 所在的直线分别为x,y,z轴建立空间直角坐标系,利用向量法能求出异面直线
所在的直线分别为x,y,z轴建立空间直角坐标系,利用向量法能求出异面直线![]() ,
,![]() 所成角的余弦值;
所成角的余弦值;![]() 求出平面
求出平面![]() 的一个法向量和平面FAD的一个法向量,利用向量法能求出面
的一个法向量和平面FAD的一个法向量,利用向量法能求出面![]() 与面FAD所成的锐二面角的余弦值.
与面FAD所成的锐二面角的余弦值.

![]() 在正四棱柱
在正四棱柱![]() 中,
中,![]() 平面ABCD,底面ABCD是正方形,
平面ABCD,底面ABCD是正方形,
所以AD,DC,![]() 两两垂直,
两两垂直,
以A为原点,DA,DC,![]() 所在的直线分别为x,y,z轴建立空间直角坐标系,
所在的直线分别为x,y,z轴建立空间直角坐标系,
又因![]() ,
,![]() ,E,F分别是棱
,E,F分别是棱![]() ,
,![]() 上的点,
上的点,
且满足![]() ,
,![]() ,
,![]() ,
,
所以![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,![]() 1,
1,![]() ,
,
所以![]() ,
,
设异面直线![]() ,
,![]() 所成角为
所成角为![]()
所以![]() ,
,
所以异面直线![]() ,
,![]() 所成角的余弦值为
所成角的余弦值为![]()
![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则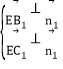 ,所以
,所以![]() ,令
,令![]() ,
,
所以![]() ,
,
平面FAD的一个法向量为![]() ,
,
则 ,所以
,所以![]() ,令
,令![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以面![]() 与面FAD所成的锐二面角的余弦值为
与面FAD所成的锐二面角的余弦值为![]()


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】《朗读者》以精美的文字,最平实的情感读出文字背后的价值,感染了众多听众,中央电视台在2018年推出了《朗读者第二季》,电视台节目组要从2018名观众中抽取50名幸运观众.先用简单随机抽样从2018人中剔除18人,剩下的2000人再按系统抽样方法抽取50人,则在2018人中,每个人被抽取的可能性 ( )
A. 都相等,且为![]() B. 都相等,且为
B. 都相等,且为![]() C. 均不相等D. 不全相等
C. 均不相等D. 不全相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() 与常数
与常数![]() ,若
,若![]() 恒成立,则称
恒成立,则称![]() 为函数
为函数![]() 的一个“
的一个“![]() 数对”;设函数
数对”;设函数![]() 的定义域为
的定义域为![]() ,且
,且![]() .
.
(Ⅰ)若![]() 是
是![]() 的一个“
的一个“![]() 数对”,且
数对”,且![]() ,求常数
,求常数![]() 的值;
的值;
(Ⅱ)若![]() 是
是![]() 的一个“
的一个“![]() 数对”,求
数对”,求![]() ;
;
(Ⅲ)若![]() 是
是![]() 的一个“
的一个“![]() 数对”,且当
数对”,且当![]() ,
, ![]() ,求
,求![]() 的值及
的值及![]() 在区间
在区间![]() 上的最大值与最小值.
上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,E,F分别为A1C1和BC的中点,M,N分别为A1B和A1C的中点.求证:
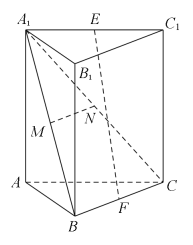
(1)MN∥平面ABC;
(2)EF∥平面AA1B1B.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com