
【题目】已知四边形ABCD为矩形,AB=2AD=4,M为AB的中点,将△ADM沿DM折起,得到四棱锥A1﹣DMBC,设A1C的中点为N,在翻折过程中,得到如下有三个命题:①BN∥平面A1DM;②三棱锥N﹣DMC的最大体积为![]() ;③在翻折过程中,存在某个位置,使得DM⊥A1C.其中正确命题的序号为_____.
;③在翻折过程中,存在某个位置,使得DM⊥A1C.其中正确命题的序号为_____.
【答案】①②
【解析】
分别延长DM,CB交于H,连接A1H,可证B为CH的中点,因此有BN∥A1H,可得①为正确;要使三棱锥N﹣DMC的体积最大,只需N到平面DMBC的距离最大,当平面A1DM⊥平面DMBC时满足,可求得此时体积为![]() ,②正确;DM=CM=2,CD=4,
,②正确;DM=CM=2,CD=4,
可得DM⊥MC,若DM⊥A1C,可证DM⊥A1M,与已知DM为斜边矛盾,③错误.
对于①,分别延长DM,CB交于H,连接A1H,如图所示;
由已知得![]() ,可得B为CH的中点,
,可得B为CH的中点,
可得BN为△A1CH的中位线,可得BN∥A1H,
BN平面A1DM,A1H平面A1DM,
可得BN∥平面A1DM∴①正确;
对于②,当平面A1DM⊥平面DMBC时,
A1到平面DMBC的距离最大,且为![]() ,
,
此时N到平面DMBC的距离最大,且为![]() ,
,
△DMC的面积为![]() 2×4=4,
2×4=4,
可得三棱锥N﹣DMC的最大体积为![]() 4
4![]() ,
,
∴②正确;
对于③,若DM⊥A1C,又DM=CM=2,CD=4,
可得DM⊥MC,则DM⊥平面A1CM,即有DM⊥A1M,
这与DM为斜边矛盾,∴③错误;
综上,以上正确命题的序号为①②.
故答案为:①②.



科目:高中数学 来源: 题型:
【题目】在下列向量组中,可以把向量![]() =(3,2)表示出来的是( )
=(3,2)表示出来的是( )
A. ![]() =(0,0),
=(0,0),![]() =(1,2)B.
=(1,2)B. ![]() =(-1,2),
=(-1,2),![]() =(5,-2)
=(5,-2)
C. ![]() =(3,5),
=(3,5),![]() =(6,10)D.
=(6,10)D. ![]() =(2,-3),
=(2,-3),![]() =(-2,3)
=(-2,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,如果存在非零常数
,如果存在非零常数![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 是“似周期函数”,非零常数
是“似周期函数”,非零常数![]() 为函数
为函数![]() 的“似周期”.现有下面四个关于“似周期函数”的命题:
的“似周期”.现有下面四个关于“似周期函数”的命题:
①如果“似周期函数”![]() 的“似周期”为-1,那么它是周期为2的周期函数;
的“似周期”为-1,那么它是周期为2的周期函数;
②函数![]() 是“似周期函数”;
是“似周期函数”;
③函数![]() 是“似周期函数”;
是“似周期函数”;
④如果函数![]() 是“似周期函数”,那么“
是“似周期函数”,那么“![]() ”.
”.
其中是真命题的序号是 .(写出所有满足条件的命题序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是数列
是数列![]() 的前
的前![]() 项和,对任意
项和,对任意![]() 都有
都有![]() 成立(其中
成立(其中![]() 是常数).
是常数).
(1)当![]() 时,求
时,求![]() :
:
(2)当![]() 时,
时,
①若![]() ,求数列
,求数列![]() 的通项公式:
的通项公式:
②设数列![]() 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“![]() 数列”,如果
数列”,如果![]() ,试问:是否存在数列
,试问:是否存在数列![]() 为“
为“![]() 数列”,使得对任意
数列”,使得对任意![]() ,都有
,都有![]() ,且
,且![]() ,若存在,求数列
,若存在,求数列![]() 的首项
的首项![]() 的所有取值构成的集合;若不存在.说明理由.
的所有取值构成的集合;若不存在.说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为 (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,过极点的两直线l1,l2相互垂直,与曲线C分别相交于A,B两点(不同于点O),且l1的倾斜角为
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,过极点的两直线l1,l2相互垂直,与曲线C分别相交于A,B两点(不同于点O),且l1的倾斜角为![]() .
.
(1)求曲线C的极坐标方程和直线l2的直角坐标方程;
(2)求△OAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
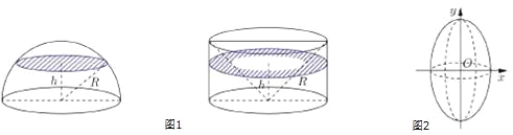
【题目】(数学文卷·2017届重庆十一中高三12月月考第16题) 现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球应用祖暅原理(图1),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为![]() ,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁是我国国家名片之一,高铁的修建凝聚着中国人的智慧与汗水.如图所示,B、E、F为山脚两侧共线的三点,在山顶A处测得这三点的俯角分别为![]() 、
、![]() 、
、![]() ,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.
,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.
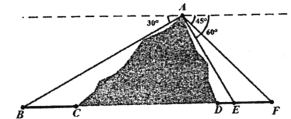
(1)求出线段AE的长度;
(2)求出隧道CD的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义![]() 上的函数
上的函数![]() ,若满足:对任意
,若满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.
的上界.
(1)设![]() ,判断
,判断![]() 在
在![]() 上是否有界函数,若是,请说明理由,并写出
上是否有界函数,若是,请说明理由,并写出![]() 的所有上界的值的集合,若不是,也请说明理由;
的所有上界的值的集合,若不是,也请说明理由;
(2)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com