D
分析:先将函数解析式写成分段函数,再结合二次函数、一次函数的单调性,考察图象与x轴交点情况,要求在(0,2)上应有两个交点,列出满足条件的不等式组再求解.
解答:f(x)=

令m=-
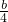
.
当m≤0时,b≥0,f(x)在(0,2)上是单调增函数,f(x)>f(0)=1>0,f(x)=0在x∈(0,2)上无解.
当0<m≤1时,0>b≥-4 ①,f(x)在(0,1)上单调递减,在(1,2)上单调递增,若方程f(x)=0在x∈(0,2)上有两个解,则须有

解得-1>b>-

.符合①式要求.
当2>m>1时,-8<b<-4,②f(x)在(0,m)上单调递减,在(m,2)上单调递增,若方程f(x)=0在x∈(0,2)上有两个解,则须有

解得b>-

.不符合②式要求.
当m≥2时,b≤-8,f(x)在(0,2)上是单调减函数,方程f(x)=0在x∈(0,2)上有不会两个解.
综上所述,实数b的取值范围是b∈
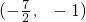
.
故选D.
点评:本题考查函数与方程,函数图象,最值,考察分类讨论、计算、数形结合的思想.

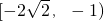
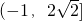
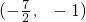
 令m=-
令m=-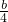 .
. 解得-1>b>-
解得-1>b>- .符合①式要求.
.符合①式要求. 解得b>-
解得b>- .不符合②式要求.
.不符合②式要求.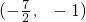 .
.
