定义:两个连续函数(图象不间断)f(x),g(x)在区间[a,b]上都有意义,我们称函数|f(x)+g(x)|在[a,b]上的最大值叫做函数f(x)与g(x)在区间[a,b]上的“绝对和”.
(1)试求函数f(x)=x2与g(x)=x(x+2)(x-4)在闭区间[-2,2]上的“绝对和”.
(2)设hm(x)=-4x+m及f(x)=x2都是定义在闭区间[1,3]上,记hm(x)与f(x)的“绝对和”为Dm,如果D(m)的最小值是D(m0),则称f(x)可用hm0(x)“替代”,试求m0的值,使f(x)可用hm0(x)“替代”.
分析:(1)令F(x)=f(x)+g(x),先讨论满足F′(x)=0的点附近的导数的符号的变化情况,来确定极值,再将F(x)的各极值与其端点的函数值比较,其中最大的一个就是最大值,最小的一个就是最小值,即可求出所求;
(2)设?(x)=hm(x)+f(x),根据二次函数的性质可知在闭区间[1,3]上,D(m)是|m-3|与|m-4|中较大者,然后求出D(m)的最小值时m的值即可.
解答:解:(1)令F(x)=f(x)+g(x)=x
2+x(x+2)(x-4)=x
3-x
2-8x,
则F'(x)=3x
2-2x-8=(3x+4)(x-2).F(x),F'(x)随x的值的变化情况如下表
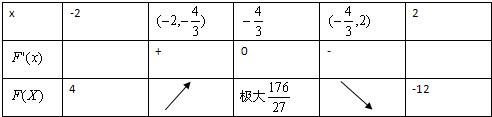
由表可知F(x)的值域为
[-12,].故|f(x)+f(x)|在[-2,2]上的最大值为12.
从而f(x)与g(x)在[-2,2]上的“绝对和”为12.
(2)设?(x)=h
m(x)+f(x)=-4x+m+x
2=(x-2)
2+m-4.
而?(1)=?(3)=m-3?∴D(m)是|m-3|与|m-4|中较大者.
∴
D(m)=∴当m=
时,D(m)最小,∴
m0=.
即
m0=时,f(x)可用
hm0(x)“替代”
点评:本题立意比较新颖,会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值,属于中档题.




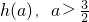 ,且h(a)=2,试求a的取值范围.
,且h(a)=2,试求a的取值范围.