
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点F到右准线的距离为3.
,右焦点F到右准线的距离为3.
(1)求椭圆C的标准方程;
(2)设过F的直线l与椭圆C相交于P,Q两点.已知l被圆O:x2+y2=a2截得的弦长为![]() ,求△OPQ的面积.
,求△OPQ的面积.
【答案】(1)![]() 1;(2)
1;(2)![]() .
.
【解析】
(1)由题可得![]() ,
,![]() ,再由
,再由![]() 可求得
可求得![]() ,即可得到椭圆方程;
,即可得到椭圆方程;
(2)显然直线![]() 的斜率不为0,设直线l的方程为x=my+1,与椭圆方程联立,则利用韦达定理可得
的斜率不为0,设直线l的方程为x=my+1,与椭圆方程联立,则利用韦达定理可得![]() 的纵坐标的关系,再根据弦长公式求得
的纵坐标的关系,再根据弦长公式求得![]() ,由直线截圆的弦长求得
,由直线截圆的弦长求得![]() ,进而求解即可.
,进而求解即可.
(1)由题意知![]() ,
,![]() ,
,
因为![]() ,解得a2=4,b2=3,
,解得a2=4,b2=3,
所以椭圆的方程为:![]() 1
1
(2)由题意知直线l的斜率不为0,由(1)知F(1,0),
设直线l的方程为x=my+1,P(x,y),Q(x',y'),
联立直线l与椭圆的方程整理得(4+3m2)y2+6my﹣9=0,
所以y+y'![]() ,yy'
,yy'![]() ,
,
所以|PQ| ,
,
因为圆O:x2+y2=4到l的距离d![]() ,被圆O:x2+y2=4截得的弦长为
,被圆O:x2+y2=4截得的弦长为![]() ,
,
所以得14=4(4![]() ),解得m2=1,
),解得m2=1,
所以d![]() ,|PQ|
,|PQ|![]() ,
,
所以S△OPQ![]() .
.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】某种大型医疗检查机器生产商,对一次性购买2台机器的客户,推出两种超过质保期后两年内的延保维修优惠方案:方案一:交纳延保金7000元,在延保的两年内可免费维修2次,超过2次每次收取维修费2000元;方案二:交纳延保金10000元,在延保的两年内可免费维修4次,超过4次每次收取维修费1000元.某医院准备一次性购买2台这种机器。现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了50台这种机器超过质保期后延保两年内维修的次数,得下表:
维修次数 | 0 | 1 | 2 | 3 |
台数 | 5 | 10 | 20 | 15 |
以这50台机器维修次数的频率代替1台机器维修次数发生的概率,记X表示这2台机器超过质保期后延保的两年内共需维修的次数。
(1)求X的分布列;
(2)以所需延保金及维修费用的期望值为决策依据,医院选择哪种延保方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某保险公司的某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | ≥4 |
保费(元) |
|
|
|
|
|
随机调查了该险种的![]() 名续保人在一年内的出险情况,得到下表:
名续保人在一年内的出险情况,得到下表:
出险次数 | 0 | 1 | 2 | 3 | ≥4 |
频数 | 280 | 80 | 24 | 12 | 4 |
该保险公司这种保险的赔付规定如下:
出险序次 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次及以上 |
赔付金额(元) |
|
|
|
|
|
将所抽样本的频率视为概率.
(1)求本年度续保人保费的平均值的估计值;
(2)按保险合同规定,若续保人在本年度内出险![]() 次,则可获得赔付
次,则可获得赔付![]() 元;依此类推,求本年度续保人所获赔付金额的平均值的估计值;
元;依此类推,求本年度续保人所获赔付金额的平均值的估计值;
(3)续保人原定约了保险公司的销售人员在上午![]() 之间上门签合同,因为续保人临时有事,外出的时间在上午
之间上门签合同,因为续保人临时有事,外出的时间在上午![]() 之间,请问续保人在离开前见到销售人员的概率是多少?
之间,请问续保人在离开前见到销售人员的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ).
).
(1)写出曲线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若射线![]() (
(![]() )与曲线
)与曲线![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() 两点(不是原点),求
两点(不是原点),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() (
(![]() )的上顶点为
)的上顶点为![]() ,离心率为
,离心率为![]() .
.
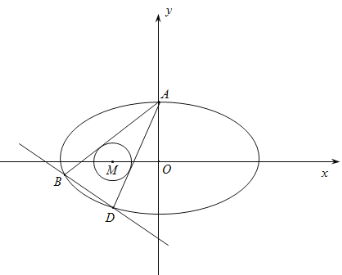
(1)求椭圆C的方程;
(2)若过点A作圆![]() (圆
(圆![]() 在椭圆C内)的两条切线分别与椭圆C相交于B,D两点(B,D不同于点A),当r变化时,试问直线BD是否过某个定点?若是,求出该定点;若不是,请说明理由.
在椭圆C内)的两条切线分别与椭圆C相交于B,D两点(B,D不同于点A),当r变化时,试问直线BD是否过某个定点?若是,求出该定点;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】低碳经济时代,文化和旅游两大产业逐渐成为我国优先发展的“绿色朝阳产业”.为了解某市的旅游业发展情况,某研究机构对该市2019年游客的消费情况进行随机调查,得到频数分布表及频率分布直方图.
旅游消费(千元) |
|
|
|
|
频数(人) | 10 | 60 |
|
|
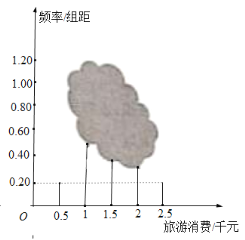
(1)由图表中数据,求![]() 的值及游客人均消费估计值(同一组中的数据以这组数据所在区间中点的值为代表)
的值及游客人均消费估计值(同一组中的数据以这组数据所在区间中点的值为代表)
(2)该机构利用最小二乘法得到2013~2017年该市的年旅游人次![]() (千万人次)与年份代码
(千万人次)与年份代码![]() 的线性回归模型:
的线性回归模型:![]() .
.
注:年份代码1~5分别对应年份2013~2017
①试求2013~2017年的年旅游人次的平均值;
②据统计,2018年该市的年旅游人次为9千万人次.建立2013~2018年该市年旅游人次![]() (千万人次)与年份代码
(千万人次)与年份代码![]() 的线性回归方程,并估计2019年该市的年旅游收入.
的线性回归方程,并估计2019年该市的年旅游收入.
注:年旅游收入=年旅游人次×人均消费
参考数据:![]() .参考公式:
.参考公式: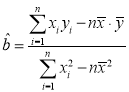 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班A、B两名学生六次数学测验成绩(百分制)如图所示:
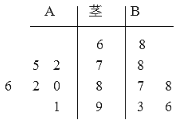
①A同学成绩的中位数大于B同学成绩的中位数;
②A同学的平均分比B同学高;
③A同学的平均分比B同学低;
④A同学成绩方差小于B同学的方差,
以上说法中正确的是( )
A.③④B.①②④C.②④D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数).在以
为参数).在以![]() 为极点、
为极点、![]() 轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,曲线
轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,曲线![]() :
:![]() 的焦点
的焦点![]() 的极坐标为
的极坐标为![]() .
.
(1)求常数![]() 的值;
的值;
(2)设![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com