
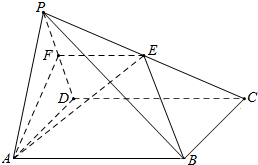
 如图,在四棱锥P-ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.分析 (Ⅰ)证明:AB∥平面PCD,即可证明AB∥EF;
(Ⅱ)利用平面PAD⊥平面ABCD,证明CD⊥AF,PA=AD,所以AF⊥PD,即可证明AF⊥平面PCD;
(Ⅲ)在(Ⅱ)的条件下,线段PB上不存在点M,使得EM⊥平面PCD.
解答  (Ⅰ)证明:因为底面ABCD是正方形,
(Ⅰ)证明:因为底面ABCD是正方形,
所以AB∥CD.
又因为AB?平面PCD,CD?平面PCD,
所以AB∥平面PCD.
又因为A,B,E,F四点共面,且平面ABEF∩平面PCD=EF,
所以AB∥EF.…(5分)
(Ⅱ)证明:在正方形ABCD中,CD⊥AD.
又因为平面PAD⊥平面ABCD,
且平面PAD∩平面ABCD=AD,
所以CD⊥平面PAD.
又AF?平面PAD
所以CD⊥AF.
由(Ⅰ)可知AB∥EF,
又因为AB∥CD,所以CD∥EF.由点E是棱PC中点,所以点F是棱PD中点.
在△PAD中,因为PA=AD,所以AF⊥PD.
又因为PD∩CD=D,所以AF⊥平面PCD.…(11分)
(Ⅲ)解:不存在. …(14分)
点评 本题考查线面平行的性质,平面与平面垂直的性质,考查线面垂直,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{23}$ | B. | $\frac{{\sqrt{23}}}{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>-1} | B. | {x|-1<x≤1} | C. | {x|-1<x<2} | D. | {x|1<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
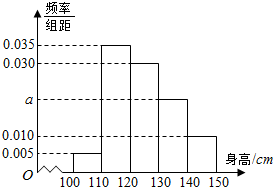 从某小学所有学生中随机抽取100名学生,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),其中样本数据分组[100,110),[110,120),[120,130),[130,140),[140,150),若要从身高在),[120,130),[130,140),[140,150)三组内的学生中,用分层抽样的方法抽取12人参加一项活动,则从身高在[130,140)内的学生中抽取的人数应为4.
从某小学所有学生中随机抽取100名学生,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),其中样本数据分组[100,110),[110,120),[120,130),[130,140),[140,150),若要从身高在),[120,130),[130,140),[140,150)三组内的学生中,用分层抽样的方法抽取12人参加一项活动,则从身高在[130,140)内的学生中抽取的人数应为4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com