
【题目】如图,已知椭圆C1: ![]() +y2=1,双曲线C2:
+y2=1,双曲线C2: ![]() =1(a>0,b>0),若以C1的长轴为直径的圆与C2的一条渐近线交于A,B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为( )
=1(a>0,b>0),若以C1的长轴为直径的圆与C2的一条渐近线交于A,B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为( ) 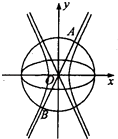
A.![]()
B.5
C.![]()
D.![]()
科目:高中数学 来源: 题型:
【题目】从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示,在这些用户中,用电量落在区间[150,250)内的户数为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三次函数f(x)=x3+bx2+cx+d(a,b,c∈R)过点(3,0),且函数f(x)在点(0,f(0))处的切线恰好是直线y=0.
(1)求函数f(x)的解析式;
(2)设函数g(x)=9x+m﹣1,若函数y=f(x)﹣g(x)在区间[﹣2,1]上有两个零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合M是R的子集,如果点x0∈R满足:a>0,x∈M,0<|x﹣x0|<a,称x0为集合M的聚点.则下列集合中以1为聚点的有( ) ① ![]() ;
;
② ![]() ;
;
③Z;
④{y|y=2x}.
A.①④
B.②③
C.①②
D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是自然对数的底数,
是自然对数的底数, ![]() .
.
(1)求![]() 的单调区间,最大值;
的单调区间,最大值;
(2)讨论关于x的方程![]() 根的个数.
根的个数.
所以当![]() 时,方程有两个根;
时,方程有两个根;
当![]() 时,方程有一两个根;
时,方程有一两个根;
当![]() 时,方程有无两个根.
时,方程有无两个根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是二次函数,顶点为(﹣1,﹣4),且与x轴的交点为(1,0).
(1)求出f(x)的解析式;
(2)求y=f(x)在区间[﹣2,2]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直角坐标平面内的两个点P和Q满足条件:①P和Q都在函数y=f(x)的图象上;②P和Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”([P,Q]与[Q,P]看作同一对“友好点对”).已知函数 ![]() ,则此函数的“友好点对”有( )
,则此函数的“友好点对”有( )
A.0对
B.1对
C.2对
D.3对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com