Question

求由直线x=1，x=2，y=0及曲线y=围成的图形的面积S.?

      

Answer 1

解：（1）分割?

       在区间［1，2］等间隔地插入n-1个点，将它等分成n个小区间：?

       ［1，］,［,］,…,［,2］，记第i个区间为［,］(i=1,2,…,n),其长度为Δx=.?

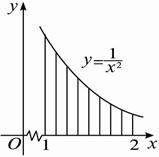
       分别过上述n-1个分点作x轴的垂线，把曲边梯形分成n个小曲边梯形（如右图），它们的面积记作：ΔS₁,ΔS₂,…,ΔS_n.则小曲边梯形面积的和为S=ΔS_i.?

       （2）近似代替?

       记=.当n很大，即Δx很小时，在区间［］上，可以认为=的值变化很小，近似地等于一个常数，不妨认为它等于f().从图形上看，就是用平行于x轴的直线段近似地代替小曲边梯形的曲边.这样，在区间［］上，用小矩形面积ΔS_i′近似地代替ΔS_i,即在局部小范围内“以直代曲”，则有?

    ΔS_i≈ΔS_i′=f()Δx?

       =?

       =(i=1,2,…,n).?

       (3)求和?

       小曲边梯形的面积和S_n=ΔS_i≈ΔS_i′?

       =?

       =n.?

       从而得到S的近似值S≈S_n=.?

       （4）取极限?

       分别将区间［1，2］等分成8，16，20，…等份时，S_n越来越趋向于S，从而有S=S_n=.

       ∴由直线x=1,x=2,y=0及曲线y=围成的图形的面积S为.?

       温馨提示：求曲边梯形的面积可以采用分割、近似代替、求和、取极限的方法来求.