
【题目】某公司为了确定下一年度投入某种产品的宣传费用,需了解年宣传费![]() (单位:万元)对年销量
(单位:万元)对年销量![]() (单位:吨)和年利润(单位:万元)的影响对近6年宣传费
(单位:吨)和年利润(单位:万元)的影响对近6年宣传费![]() 和年销量
和年销量![]() 的数据做了初步统计,得到如下数据:
的数据做了初步统计,得到如下数据:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年宣传费 | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量 | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() ,两边取对数,即
,两边取对数,即![]() ,令
,令![]() ,即
,即 对上述数据作了初步处理,得到相关的值如下表:
对上述数据作了初步处理,得到相关的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(1)从表中所给出的6年年销售量数据中任选2年做年销售量的调研,求所选数据中至多有一年年销售量低于21吨的概率.
(2)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若生产该产品的固定成本为200(万元),且每生产1(吨)产品的生产成本为20(万元)(总成本=固定成本+生产成本+年宣传费),销售收入为![]() (万元),假定该产品产销平衡(即生产的产品都能卖掉),2019年该公司计划投入108万元宣传费,你认为该决策合理吗?请说明理由.(其中
(万元),假定该产品产销平衡(即生产的产品都能卖掉),2019年该公司计划投入108万元宣传费,你认为该决策合理吗?请说明理由.(其中![]() 为自然对数的底数,
为自然对数的底数,![]() )
)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为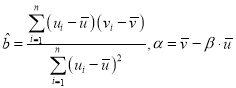
【答案】(1)![]() (2)
(2)![]() (3)不合理,见解析
(3)不合理,见解析
【解析】
(1)由表中数据可知6年中有3年的年销量低于21吨,则“至多有一年年销量低于21吨”的选法有![]() 种选法,从而可求其概率.
种选法,从而可求其概率.
(2)由题中数据得:![]() ,
,![]() ,根据
,根据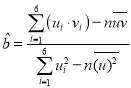 ,先求出
,先求出![]() ,由
,由![]() ,从而得出
,从而得出![]() ,得出方程.
,得出方程.
(3)根据题意有公司的年利润为![]() ,求出2019年该公司利润的最大值,
,求出2019年该公司利润的最大值,
(1)记事件A表示“至多有一年年销量低于21吨”,由表中数据可知6年中有3年的年销量低于21吨,故
![]()
(2)对![]() 两边取对数得
两边取对数得![]() ,令
,令![]() 得
得![]() ,由题中数据得:
,由题中数据得:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以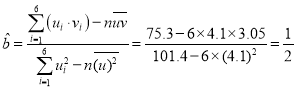 ,
,
由![]() ,
,
得![]() ,故所求回归方程为
,故所求回归方程为![]()
(3)设该公司的年利润为![]() ,因为利润/span>=销售收入-总成本,所以由题意可知
,因为利润/span>=销售收入-总成本,所以由题意可知
![]() 当
当![]() 即
即![]() 时,利润
时,利润![]() 取得最大值500万元,
取得最大值500万元,
所以当宣传费![]() 时,利润
时,利润![]() 取得最大值.
取得最大值.
故2019年该公司计划投入108万元宣传费的决策不合理


科目:高中数学 来源: 题型:
【题目】已知函数![]() 有如下性质:如果常数
有如下性质:如果常数![]() ,那么该函数在
,那么该函数在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
(1)已知![]() ,利用上述性质,求函数
,利用上述性质,求函数![]() 的单调区间和值域;
的单调区间和值域;
(2)对于(1)中的函数![]() 和函数
和函数![]() ,若对任意
,若对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为了解学生对学校食堂服务的满意度,随机调查了50名男生和50名女生,每位学生对食堂的服务给出满意或不满意的评价,得到如图所示的列联表.经计算![]() 的观测值
的观测值![]() ,则可以推断出( )
,则可以推断出( )
满意 | 不满意 | |
男 | 30 | 20 |
女 | 40 | 10 |
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
A.该学校男生对食堂服务满意的概率的估计值为![]()
B.调研结果显示,该学校男生比女生对食堂服务更满意
C.有95%的把握认为男、女生对该食堂服务的评价有差异
D.有99%的把握认为男、女生对该食堂服务的评价有差异
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂在两个车间![]() ,
,![]() 内选取了12个产品,它们的某项指标分布数据的茎叶图如图所示,该项指标不超过19的为合格产品.
内选取了12个产品,它们的某项指标分布数据的茎叶图如图所示,该项指标不超过19的为合格产品.
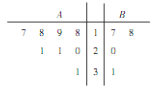
(1)从选取的产品中在两个车间分别随机抽取2个产品,求两车间都至少抽到一个合格产品的概率;
(2)若从车间![]() ,
,![]() 选取的产品中随机抽取2个产品,用
选取的产品中随机抽取2个产品,用![]() 表示车间
表示车间![]() 内产品的个数,求
内产品的个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,△ABC是正三角形,AD=CD.
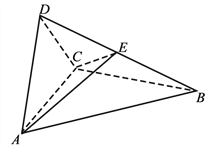
(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.

(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年9月第三个公休日是全国科普日.某校为迎接2019年全国科普日,组织了科普知识竞答活动,要求每位参赛选手从4道“生态环保题”和2道“智慧生活题”中任选3道作答(每道题被选中的概率相等),设随机变量ξ表示某选手所选3道题中“智慧生活题”的个数.
(Ⅰ)求该选手恰好选中一道“智慧生活题”的概率;
(Ⅱ)求随机变量ξ的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com